
分析 设B(0,yB),C(0,yC),A(x0,y0),其中x0>2,写出直线AB的方程为(y0-yB)x-x0y+x0yB=0,由直线AB与圆相切可得(x0-2)yB2+2y0yB-x0=0,同理:(x0-2)yA2+2y0yA-x0=0,故yA,yB是方程(x0-2)y2+2y0y-x0=0的两个不同的实根,因为S=$\frac{1}{2}$|yC-yB|x0,再结合韦达定理即可求出三角形的最小值.
解答 解:设B(0,yB),C(0,yC),A(x0,y0),其中x0>2,
所以直线AB的方程,化简得(y0-yB)x-x0y+x0yB=0
直线AB与圆相切,圆心到直线的距离等于半径,两边平方化简得(x0-2)yB2+2y0yB-x0=0
同理可得:(x0-2)yA2+2y0yA-x0=0,
故yC,yB是方程(x0-2)y2+2y0y-x0=0的两个不同的实根,
所以yC+yB=$\frac{2{y}_{0}}{2-{x}_{0}}$,yCyB=$\frac{{x}_{0}}{2-{x}_{0}}$,
所以S=$\frac{1}{2}$|yC-yB|x0=$\frac{{{x}_{0}}^{2}}{{x}_{0}-2}$=(x0-2)+$\frac{4}{{x}_{0}-2}$+4≥8,
所以当且仅当x0=4时,S取到最小值8,
所以△ABC的面积的最小值为8.
故答案为:8.
点评 本题主要考查直线与抛物线的位置关系,以及直线与圆的位置关系,正确利用韦达定理是解题的关键.


 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 9 | B. | -9 | C. | 7 | D. | -7 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
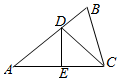 如图,设△ABC的个内角A、B、C对应的三条边分别为a、b、c,且角A、B、C成等差数列,a=2,线段AC的垂直平分线分别交线段AB、AC于D、E两点.
如图,设△ABC的个内角A、B、C对应的三条边分别为a、b、c,且角A、B、C成等差数列,a=2,线段AC的垂直平分线分别交线段AB、AC于D、E两点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
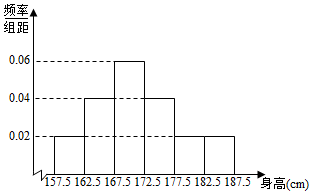 某省高中男生身高统计调查数据显示:全省100000名男生的身高服从正态分布N(170.5,16).现从某学校高三年级男生中随机抽取50名测量身高,测量发现被测学生身高全部介于157.5cm和187.5cm之间,将测量结果按如下方式分成6组:第1组[157.5,162.5),第2组[162.5,167.5),…,第6组[182.5,187.5],如图是按上述分组方法得到的频率分布直方图.
某省高中男生身高统计调查数据显示:全省100000名男生的身高服从正态分布N(170.5,16).现从某学校高三年级男生中随机抽取50名测量身高,测量发现被测学生身高全部介于157.5cm和187.5cm之间,将测量结果按如下方式分成6组:第1组[157.5,162.5),第2组[162.5,167.5),…,第6组[182.5,187.5],如图是按上述分组方法得到的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | 2 | C. | 2$\sqrt{2}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 20 | B. | 14 | C. | 10 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com