
已知函数f(x)=3x,且f(a+2)=18,g(x)=3ax-4x的定义域为区间[-1,1].
(1)求g(x)的解析式;
(2)判断g(x)的单调性.
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:高中数学 来源: 题型:解答题
已知定义域为R的函数f(x)满足f(f(x)-x2+x)=f(x)-x2+x.
(Ⅰ)若f(2)=3,求f(1);又若f(0)=a,求f(a);
(Ⅱ)设有且仅有一个实数x0,使得f(x0)= x0,求函数f(x)的解析表达式.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
函数f(x)=2x和g(x)=x3的图象的示意图如右图所示,设两函数的图象交于点A(x1,y1),B(x2,y2),且x1<x2.
(1)请指出示意图中曲线C1,C2分别对应哪一个函数?
(2)若x1∈,x2∈,且a,b∈{1,2,3,4,5,6,7,8,9,10,11,12}指出a,b的值,并说明理由;
(3)结合函数图象示意图,判断f(6),g(6),f(2010),g(2010)的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,二次函数 (
( )的图象与反比例函数
)的图象与反比例函数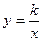 图象相交于点
图象相交于点 ,已知点
,已知点 的坐标为
的坐标为 ,点
,点 在第三象限内,且
在第三象限内,且 的面积为
的面积为 (
( 为坐标原点)
为坐标原点)
① 求实数 的值;
的值;
② 求二次函数 (
( )的解析式;
)的解析式;
③ 设抛物线与 轴的另一个交点为
轴的另一个交点为 ,
, 点为线段
点为线段
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题8分)经过调查发现,某种新产品在投 放市场的30天中,前20天其价格直线上升,后10天价格呈直线下降趋势。现抽取其中4天的价格如下表所示:
放市场的30天中,前20天其价格直线上升,后10天价格呈直线下降趋势。现抽取其中4天的价格如下表所示:
| 时间 | 第4天 | 第12天 | 第20天 | 第28天 |
| 价格 (千元) | 34 | 42 | 50 | 34 |
 关于时间
关于时间 的函数表达式(
的函数表达式( 表示投放市场的第
表示投放市场的第 天)
天) 与时间
与时间 的函数关系式为
的函数关系式为 :
: ,问该产品投放市场第几天,日销售额最高?
,问该产品投放市场第几天,日销售额最高?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com