
已知定义域为R的函数f(x)满足f(f(x)-x2+x)=f(x)-x2+x.
(Ⅰ)若f(2)=3,求f(1);又若f(0)=a,求f(a);
(Ⅱ)设有且仅有一个实数x0,使得f(x0)= x0,求函数f(x)的解析表达式.
解:(Ⅰ)因为对任意x∈R,有f(f(x)-x2 + x)=f(x)- x2 +x,
所以f(f(2)- 22+2)=f(2)-22+2.
又由f(2)=3,得f(3-22+2)-3-22+2,即f(1)=1.
若f(0)=a,则f(a-02+0)=a-02+0,即f(a)=a.
(Ⅱ)因为对任意x∈R,有f(f(x))-x2 +x)=f(x)-x2 +x.
又因为有且只有一个实数x0,使得f(x0)- x0.所以对任意xεR,有f(x)-x2 +x= x0.
在上式中令x= x0,有f(x0)-x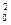 + x0= x0,
+ x0= x0,
又因为f(x0)- x0,所以x0-x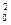 =0,故x0=0或x0=1.
=0,故x0=0或x0=1.
若x0=0,则f(x)- x2 +x=0,即f(x)= x2-x.
但方程x2-x=x有两上不同实根,与题设条件矛质,故x2≠0.
若x2=1,则有f(x)-x2 +x=1,即f(x)= x2-x+1.易验证该函数满足题设条件.
综上,所求函数为f(x)= x2-x+1(x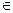 R)
R)
解析


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:高中数学 来源: 题型:解答题
已知函数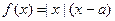 ,
,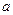 为实数.
为实数.
(1)当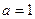 时,判断函数
时,判断函数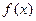 的奇偶性,并说明理由;
的奇偶性,并说明理由;
(2)当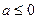 时,指出函数
时,指出函数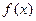 的单调区间(不要过程);
的单调区间(不要过程);
(3)是否存在实数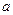
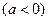 ,使得
,使得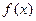 在闭区间
在闭区间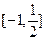 上的最大值为2.若存在,求出
上的最大值为2.若存在,求出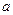 的值;若不存在,请说明理由
的值;若不存在,请说明理由
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某企业生产一种产品时,固定成本为5 000元,而每生产100台产品时直接消耗成本要增加2 500元,市场对此商品年需求量为500台,销售的收入函数为
500元,市场对此商品年需求量为500台,销售的收入函数为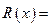
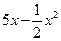 (万元)(0≤
(万元)(0≤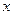 ≤5),其中
≤5),其中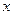 是产品售出的数量(单位:百台)
是产品售出的数量(单位:百台)
(1)把利润表示为年产量的函数;(2)年产量多少时,企业所得的利润最大;
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题13分)已知函数 与
与 的图象相交于
的图象相交于 ,
, ,
, ,
, 分别是
分别是 的图象在
的图象在 两点的切线,
两点的切线, 分别是
分别是 ,
, 与
与 轴的交点.
轴的交点.
(1)求 的取值范围;
的取值范围;
(2)设 为点
为点 的横坐标,当
的横坐标,当 时,写出
时,写出 以
以 为自变量的函数式,并求其定义域和值域;
为自变量的函数式,并求其定义域和值域;
(3)试比较 与
与 的大小,并说明理由(
的大小,并说明理由( 是坐标原点).
是坐标原点).
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)已知二次函数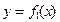 的
的 图象以原点为顶点且过点(1,1),反比例函数
图象以原点为顶点且过点(1,1),反比例函数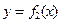 的图象与直线
的图象与直线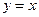 的两个交点间的距离为8,
的两个交点间的距离为8,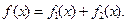
(1)求函数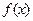 的表达式;
的表达式;
(2)证明:当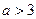 时,关于
时,关于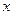 的方程
的方程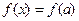 有三个实数解.
有三个实数解.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数f(x)=3x,且f(a+2)=18,g(x)=3ax-4x的定义域为区间[-1,1].
(1)求g(x)的解析式;
(2)判断g(x)的单调性.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com