
函数f(x)=2x和g(x)=x3的图象的示意图如右图所示,设两函数的图象交于点A(x1,y1),B(x2,y2),且x1<x2.
(1)请指出示意图中曲线C1,C2分别对应哪一个函数?
(2)若x1∈,x2∈,且a,b∈{1,2,3,4,5,6,7,8,9,10,11,12}指出a,b的值,并说明理由;
(3)结合函数图象示意图,判断f(6),g(6),f(2010),g(2010)的大小.
(1)C1对应的函数为g(x)=x3,C2对应的函数为f(x)=2x.
(2)a=1,b=9.
理由如下:
令φ(x)=f(x)-g(x)=2x-x3,则x1,x2为函数φ(x)的零点.
∵φ(1)=1>0,φ(2)=-4<0,φ(9)=29-93<0,φ(10)=210-103>0,
∴方程φ(x)=f(x)-g(x)的两个零点x1∈(1,2),x2∈(9,10)
因此整数a=1,b=9.
(3)从图象上可以看出,当x1<x<x2时,f(x)<g(x),
∴f(6)<g(6).
当x>x2时,f(x)>g(x),∴g(2010)<f(2010).
∵g(6)<g(2010),
∴f(6)<g(6)<g(2010)<f(2010).
解析


科目:高中数学 来源: 题型:解答题
已知函数f(x)=3x,且f(a+2)=18,g(x)=3ax-4x的定义域为区间[-1,1].
(1)求g(x)的解析式;
(2)判断g(x)的单调性.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某企业生产一种产品时,固定成本为5000元,而每生产100台产品时直接消耗成本要增加2500元,市场对此商品年需求量为500台,销售的收入函数为R(x)=5x-x2(万元)(0≤x≤5),其中x是产品售出的数量(单位:百台)
(1)把利润表示为年产量的函数;
(2)年产量多少时,企业所得的利润最大?
(3)年产量多少时,企业才不亏本?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数 ,当
,当 恒成立的a的最小值为k,存在n个
恒成立的a的最小值为k,存在n个
正数 ,且
,且 ,任取n个自变量的值
,任取n个自变量的值
(I)求k的值;
(II)如果
(III)如果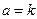 ,且存在n个自变量的值
,且存在n个自变量的值 ,使
,使 ,求证:
,求证:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com