
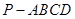 的底面
的底面 是矩形,
是矩形,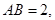
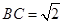 ,且侧面
,且侧面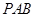 是正三角形,平面
是正三角形,平面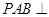 平面
平面 ,
,
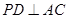 ;
;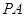 上是否存在一点
上是否存在一点 ,使得二面角
,使得二面角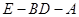 的大小为45°.若存在,试求
的大小为45°.若存在,试求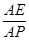 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.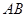 中点
中点 ,由
,由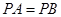 ,得
,得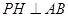 ,又平面
,又平面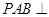 平面
平面 ,且平面
,且平面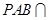 平面
平面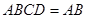 ,所以
,所以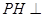 平面
平面 ,然后以
,然后以 为原点,建立空间直角坐标系
为原点,建立空间直角坐标系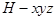 ,结合向量的数量积公式
,结合向量的数量积公式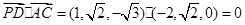 得到证明。
得到证明。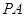 上存在一点
上存在一点 ,不妨设
,不妨设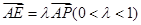 ,
, 的坐标为
的坐标为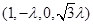 则得到平面
则得到平面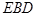 的一个法向量
的一个法向量 .,
.,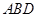 的法向量可以是
的法向量可以是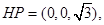 向量的夹角公式,表示出二面角,从而解得。
向量的夹角公式,表示出二面角,从而解得。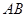 中点
中点 ,则由
,则由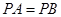 ,得
,得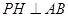 ,又平面
,又平面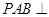 平面
平面 ,且平面
,且平面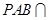 平面
平面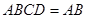 ,所以
,所以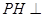 平面
平面 .以
.以 为原点,建立空间直角坐标系
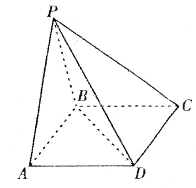
为原点,建立空间直角坐标系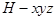 (如图).则
(如图).则 ……………………………2分
……………………………2分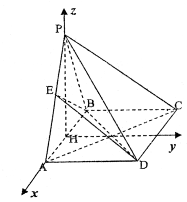
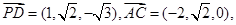
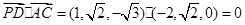 ,
,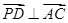 ,即
,即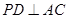 .…………………………………6分
.…………………………………6分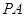 上存在一点
上存在一点 ,不妨设
,不妨设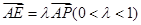 ,
, 的坐标为
的坐标为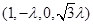 ,……………………………8分
,……………………………8分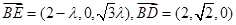
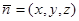 是平面
是平面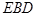 的法向量,则
的法向量,则
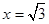 ,则得到平面
,则得到平面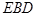 的一个法向量
的一个法向量 .…………………10分
.…………………10分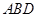 的法向量可以是
的法向量可以是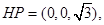
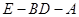 的大小等于45°,
的大小等于45°,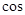 45°=
45°=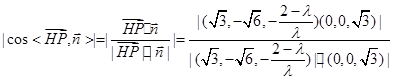
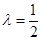 ,即
,即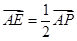
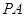 上存在点
上存在点 ,当
,当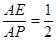 时,使得二面角
时,使得二面角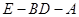 的大小等于45°. ………12分
的大小等于45°. ………12分

 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案科目:高中数学 来源:不详 题型:解答题
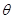 的值;若不能确定,说明理由.
的值;若不能确定,说明理由.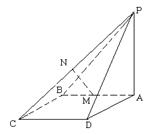
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
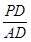 =
=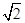 ,求平面PBE与平面ABCD所成的锐二面角的大小.
,求平面PBE与平面ABCD所成的锐二面角的大小.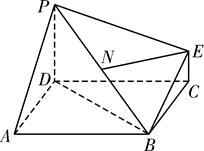
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
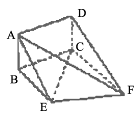
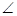 BCF=
BCF=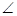 CEF=
CEF=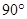 ,AD=
,AD=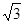 ,EF=2.
,EF=2.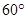 .
.
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
A.如果平面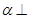 平面 平面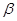 ,那么平面 ,那么平面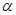 内一定存在直线平行于平面 内一定存在直线平行于平面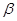 ; ; |
B.如果平面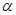 不垂直于平面 不垂直于平面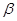 ,那么平面 ,那么平面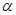 内一定不存在直线垂直于平面 内一定不存在直线垂直于平面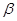 ; ; |
C.如果平面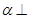 平面 平面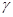 ,平面 ,平面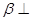 平面 平面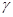 , ,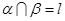 ,那么 ,那么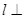 平面 平面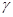 ; ; |
D.如果平面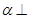 平面 平面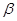 ,那么平面 ,那么平面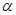 内所有直线都垂直于平面 内所有直线都垂直于平面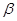 。 。 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
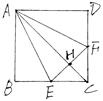
A.AG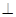 平面EFG 平面EFG | B.AH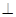 平面EFG 平面EFG | C.GF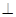 平面AEF 平面AEF | D.GH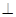 平面AEF 平面AEF |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
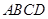 为矩形,且
为矩形,且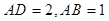 ,
,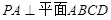 ,
,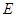 为
为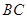 上的动点。
上的动点。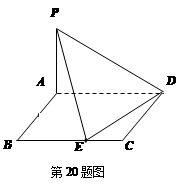
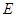 为
为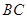 的中点时,求证:
的中点时,求证: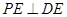 ;
;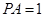 ,在线段
,在线段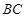 上存在这样的点E,使得二面角
上存在这样的点E,使得二面角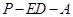 的平面角大小为
的平面角大小为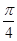 。试确定点E的位置。
。试确定点E的位置。查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com