阅读快车系列答案科目：高中数学 来源：2016-2017学年江西省南昌市高一上学期期末考试数学试卷（解析版） 题型：解答题
已知
，其最小值为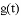
.
（1）求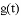的表达式；
（2）当
时，要使关于
的方程
有一个实根，求实数
的取值范围.
查看答案和解析>>
科目：高中数学 来源：2017届河北省石家庄市高三第二次质量检测数学（文）试卷（解析版） 题型：解答题
选修4-5：不等式选讲
设函数
的最大值为
．
（1）作出函数
的图象；
（2）若
，求
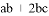的最大值．
查看答案和解析>>
科目：高中数学 来源：2017届河北省石家庄市高三第二次质量检测数学（文）试卷（解析版） 题型：选择题
李冶(1192-1279)，真定栾城（今属河北石家庄市）人，金元时期的数学家、诗人、晚年在封龙山隐居
讲学，数学著作多部，其中《益古演段》主要研究平面图形问题：求圆的直径，正方形的边长等，其中一问：现有正方形方田一块，内部有一个圆形水池，其中水池的边缘与方田四边之间的面积为
亩，若方田的四边到水池的最近距离均为二十步，则圆池直径和方田的边长分别是（注：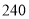 
平方步为
亩，圆周率按
近似计算）
A. 
步、
步 B. 
步、
步 C. 
步、
步 D. 
步、
步
查看答案和解析>>
科目：高中数学 来源：2017届广西南宁市高三上学期期末考试数学（理）试卷（解析版） 题型：解答题
已知曲线
的参数方程为
（
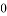为参数），以坐标原点为极点，
轴的正半轴为极轴建立极坐标系，曲线
的极坐标方程为
．
（Ⅰ）把的参数方程式化为普通方程，的极坐标方程式化为直角坐标方程；
（Ⅱ）求与交点的极坐标
．
查看答案和解析>>
科目：高中数学 来源：2017届广西南宁市高三上学期期末考试数学（理）试卷（解析版） 题型：选择题
已知
，
是函数
图像上的两个不同点.且在
两点处的切线互相平行，则
的取值范围是（ ）
A.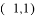 
B. 
C. 
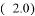D. 
查看答案和解析>>
科目：高中数学 来源：2017届河北省张家口市高三上学期期末考试数学（理）试卷（解析版） 题型：选择题
设椭圆
与直线
相交于
，
两点，若在椭圆上存在点
，使得直线
，
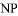斜率之积为
，则椭圆离心率为（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中数学 来源：2016-2017学年辽宁省庄河市高一上学期期末考试理数试卷（解析版） 题型：填空题
设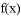
是定义在
上的奇函数，当
时，
（
为自然对数的底数），则
的值为__________．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
的的前
项和为
，对
，有
．
，设
的前
，求证：
．
，
，若向量
与向量
的夹角为
，则
=（ ）
B. 
C. 
D. 