练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】椭圆 + =1（a＞b＞0）的左、右顶点分别是A，B，左、右焦点分别是F1 ， F2 ． 若|AF1|，|F1F2|，|F1B|成等比数列，则此椭圆的离心率为 ．

    【答案】
    【解析】解：因为椭圆 + =1（a＞b＞0）的左、右顶点分别是A，B，左、右焦点分别是F1 ， F2 ．
    若|AF1|，|F1F2|，|F1B|成等比数列，|AF1|=a﹣c，|F1F2|=2c，|F1B|=a+c，
    所以（a﹣c）（a+c）=4c2 ， 即a2=5c2 ，
    所以e= ．
    所以答案是： ．
    【考点精析】解答此题的关键在于理解等比数列的基本性质的相关知识，掌握{an}为等比数列，则下标成等差数列的对应项成等比数列;{an}既是等差数列又是等比数列== {an}是各项不为零的常数列．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知集合集合，集合，且集合D满足.

    （1）求实数a的值.

    （2）对集合，其中，定义由中的元素构成两个相应的集合:,,其中是有序实数对，集合S和T中的元素个数分别为和，若对任意的,总有，则称集合具有性质P.

    ①请检验集合是否具有性质P，并对其中具有性质P的集合，写出相应的集合S和T.

    ②试判断m和n的大小关系，并证明你的结论.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知集合M＝{x|x<－3，或x>5}，P＝{x|(x－a)·(x－8)≤0}．

    (1)求M∩P＝{x|5<x≤8}的充要条件；

    (2)求实数a的一个值，使它成为M∩P＝{x|5<x≤8}的一个充分但不必要条件．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知定义域为的函数（常数，为自然对数的底数）.

    （Ⅰ）求函数的单调区间；

    （Ⅱ）若恒成立，求实数的最大整数值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】选修4-4：坐标系与参数方程

    在平面直角坐标系中，曲线参数方程为（为参数，），以坐标原点为极点，以轴正半轴为极轴，建立极坐标系，曲线的极坐标方程为.

    （Ⅰ）写出曲线的普通方程和曲线的直角坐标方程；

    （Ⅱ）已知点，曲线和曲线交于，两点，且，求实数的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】
    （1）（坐标系与参数方程选做题）曲线C的直角坐标方程为x2+y2﹣2x=0，以原点为极点，x轴的正半轴为极轴建立积坐标系，则曲线C的极坐标方程为 ．
    （2）（不等式选做题）在实数范围内，不等式|2x﹣1|+|2x+1|≤6的解集为 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在三棱柱ABC﹣A1B1C1中，已知AB=AC=AA1= ，BC=4，点A1在底面ABC的投影是线段BC的中点O．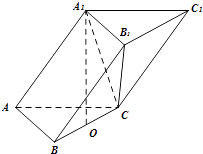

    （1）证明在侧棱AA1上存在一点E，使得OE⊥平面BB1C1C，并求出AE的长；
    （2）求平面A1B1C与平面BB1C1C夹角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在△ABC中，已知 ．
    （1）求证：tanB=3tanA；
    （2）若cosC= ，求A的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在三棱柱中，底面，，，，分别为的中点，为侧棱上的动点

    （Ⅰ）求证：平面平面；

    （Ⅱ）若为线段的中点，求证：平面；

    （Ⅲ）试判断直线与平面是否能够垂直。若能垂直，求的值；若不能垂直，请说明理由

    查看答案和解析>>

    同步练习册答案