
 如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,∠ADC=45°,AD=AC=1,O为AC的中点,PO⊥平面ABCD,PO=1,M为PD的中点.
如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,∠ADC=45°,AD=AC=1,O为AC的中点,PO⊥平面ABCD,PO=1,M为PD的中点.分析 (1)要证明PB∥平面ACM,利用线面平行的判定定理,证明MO∥PB即可;
(2)取DO的中点N,连结MN,AN,则MN∥PO,推导出∠MAN=α为所求的直线AM与平面ABCD所成的角,从而求出sinα
解答 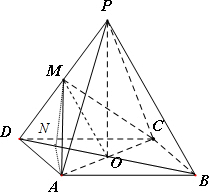 解:(1)证明:连接BD,MO,
解:(1)证明:连接BD,MO,
由题O为BD中点,又M为PD中点
∴MO∥PB,
又∵PB?面MAC,MO?面MAC,
∴PB∥面MAC
(2)取DO的中点N,连结MN,AN,则MN∥PO,
∵PO⊥平面ABCD,∴MN⊥平面ABCD,
∴∠MAN=α为所求的直线AM与平面ABCD所成的角.
MN=$\frac{1}{2}PO=\frac{1}{2}$.
在Rt△ADO中,∵DO=$\sqrt{{1}^{2}+(\frac{1}{2})^{2}}=\frac{\sqrt{5}}{2}$,AN=$\frac{1}{2}DO=\frac{\sqrt{5}}{4}$.
在Rt△AMN中,AM=$\sqrt{M{N}^{2}+A{N}^{2}}=\frac{3}{4}$,
∴sinα=$\frac{MN}{AM}$=$\frac{2}{3}$.
点评 本题考查线面平行的证明,考查线面角的正弦值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{3}{7}$ | C. | $\frac{1}{2}$ | D. | $\frac{4}{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1:1 | B. | 2:1 | C. | 3:1 | D. | 4:1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在东辰学校的职工食堂中,食堂每天以3元/个的价格从面包店购进面包,然后以5元/个的价格出售.如果当天卖不完,剩下的面包以1元/个的价格卖给饲料加工厂.根据以往统计资料,得到食堂每天面包需求量的频率分布直方图如下图所示.食堂某天购进了90个面包,以x(单位:个,60≤x≤110)表示面包的需求量,T(单位:元)表示利润.
在东辰学校的职工食堂中,食堂每天以3元/个的价格从面包店购进面包,然后以5元/个的价格出售.如果当天卖不完,剩下的面包以1元/个的价格卖给饲料加工厂.根据以往统计资料,得到食堂每天面包需求量的频率分布直方图如下图所示.食堂某天购进了90个面包,以x(单位:个,60≤x≤110)表示面包的需求量,T(单位:元)表示利润.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com