
分析 根据${({x+2\sqrt{x}+1})^4}$表示4个因式$({x+2\sqrt{x}+1})$的乘积,利用组合的知识,分类讨论,求得x3的系数.
解答 解:∵${({x+2\sqrt{x}+1})^4}$表示4个因式$({x+2\sqrt{x}+1})$的乘积,
x3的系数可以是:从4个因式中选三个因式提供x,另一个因式中有一个提供1;
也可以是从3个因式中选两个因式都提供x,其余的两个提供$2\sqrt{x}$,可得x3的系数,
故x3的系数为:$C_4^3+C_4^2•{2^2}=28$,
故答案为:28.
点评 本题主要考查二项式定理的应用,二项式表示的意义,属于基础题.


科目:高中数学 来源: 题型:解答题
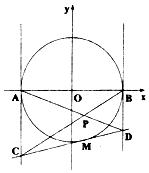 已知圆O:x2+y2=4与x轴交于A,B两点,点M为圆O上异于A,B的任意一点,圆O在点M处的切线与圆O在点A,B处的切线分别交于C,D,直线AD和BC交于点P,设P点的轨迹为曲线E.
已知圆O:x2+y2=4与x轴交于A,B两点,点M为圆O上异于A,B的任意一点,圆O在点M处的切线与圆O在点A,B处的切线分别交于C,D,直线AD和BC交于点P,设P点的轨迹为曲线E.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com