
已知函数 .
.
(I)求函数 的单调区间;
的单调区间;
(II)若函数 上是减函数,求实数
上是减函数,求实数 的最小值;
的最小值;
(III)若 ,使
,使 成立,求实数
成立,求实数 的取值范围.
的取值范围.
(I) (II)
(II) (III)
(III)
解析试题分析:由已知函数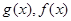 的定义域均为
的定义域均为 ,且
,且 .
.
(Ⅰ)函数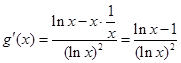 ,
,
当 时,
时,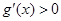 .所以函数
.所以函数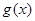 的单调增区间是
的单调增区间是 . 3分
. 3分
(Ⅱ)因f(x)在 上为减函数,故
上为减函数,故 在
在 上恒成立.
上恒成立.
所以当 时,
时,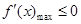 .
.
又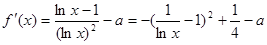 ,
,
故当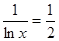 ,即
,即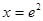 时,
时,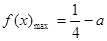 ,所以
,所以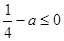 ,故
,故
所以 的最小值为
的最小值为 .
.
(Ⅲ)“若 ,使
,使 成立”等价于
成立”等价于
“当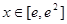 时,有
时,有 ”,
”,
有(Ⅱ),当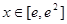 时,有
时,有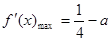 ,
,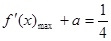 ,
,
问题等价于:“当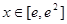 时,有
时,有 ”
”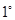 当
当 时,由(Ⅱ),
时,由(Ⅱ), 在
在 上为减函数.
上为减函数.
则 ,故
,故 .
. 当
当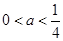 时,由于
时,由于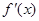
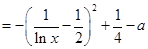 在
在 上为增函数,
上为增函数,
故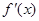 的值域为
的值域为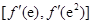 ,即
,即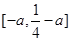 .
.
由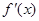 的单调性和值域知,
的单调性和值域知, 唯一
唯一 ,使
,使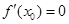 ,且满足:
,且满足:
当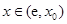 时,
时,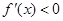 ,
, 为减函数;
为减函数;
当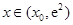 时,
时, ,
, 为增函数;
为增函数;
所以,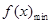 =
=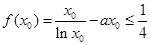 ,
, .
.
所以,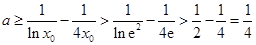 ,与
,与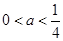 矛盾,不合题意.
矛盾,不合题意.
综上, .
.
考点:利用导数求闭区间上函数的最值;利用导数研究函数的单调性.
点评:本题考查导数知识的运用,考查函数的单调性与最值,考查恒成立问题,同时考查不等式的证明,解题的关键是正确求导数,确定函数的单调性.


科目:高中数学 来源: 题型:解答题
设函数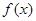 是定义在区间
是定义在区间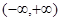 上的偶函数,且满足
上的偶函数,且满足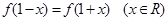
(1)求函数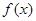 的周期;
的周期;
(2)已知当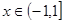 时,
时,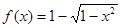 .求使方程
.求使方程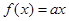 在
在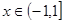 上有两个不相等实根的
上有两个不相等实根的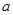 的取值集合M.
的取值集合M.
(3)记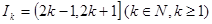 ,
,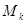 表示使方程
表示使方程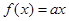 在
在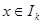 上有两个不相等实根的
上有两个不相等实根的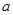 的取值集合,求集合
的取值集合,求集合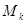 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数f(x)=x|x-a|-lnx,a∈R.
(Ⅰ)若a=1,求函数f(x)在区间[1,e]上的最大值;
(Ⅱ)若f(x)>0恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
若函数 都在区间
都在区间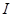 上有定义,对任意
上有定义,对任意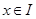 ,都有
,都有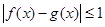 成立,则称函数
成立,则称函数 为区间
为区间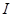 上的“伙伴函数”
上的“伙伴函数”
(1)若 为区间
为区间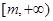 上的“伙伴函数”,求
上的“伙伴函数”,求 的范围。
的范围。
(2)判断 是否为区间
是否为区间 上的“伙伴函数”?
上的“伙伴函数”?
(3)若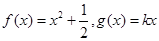 为区间
为区间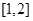 上的“伙伴函数”,求
上的“伙伴函数”,求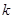 的取值范围
的取值范围
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com