
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | ¬P:?x∈(-∞,1)∪(2,+∞),x2-2x-1>0 | B. | ¬P:?x∈[1,2],x2-2x-1>0 | ||
| C. | ¬P:?x∈(-∞,1)∪(2,+∞),x2-2x-1≤0 | D. | ¬P:?x∈[1,2],x2-2x-1≤0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 态度 调查人群 | 应该取消 | 应该保留 | 无所谓 |
| 在校学生 | 2100人 | 120人 | y人 |
| 社会人士 | 500人 | x人 | z人 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
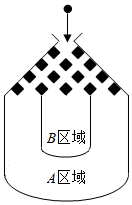 如图,将一个半径适当的小球放入容器上方的入口处,小球自由下落,小球在下落的过程中,将遇到黑色障碍物3次,最后落入A区域或B区域中,已知小球每次遇到障碍物时,向左、右两边下落的概率都是$\frac{1}{2}$.
如图,将一个半径适当的小球放入容器上方的入口处,小球自由下落,小球在下落的过程中,将遇到黑色障碍物3次,最后落入A区域或B区域中,已知小球每次遇到障碍物时,向左、右两边下落的概率都是$\frac{1}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$或-1 | B. | 2或-1 | C. | 2或1 | D. | 1或-1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com