
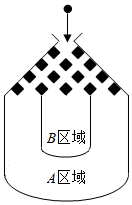
 如图,将一个半径适当的小球放入容器上方的入口处,小球自由下落,小球在下落的过程中,将遇到黑色障碍物3次,最后落入A区域或B区域中,已知小球每次遇到障碍物时,向左、右两边下落的概率都是$\frac{1}{2}$.
如图,将一个半径适当的小球放入容器上方的入口处,小球自由下落,小球在下落的过程中,将遇到黑色障碍物3次,最后落入A区域或B区域中,已知小球每次遇到障碍物时,向左、右两边下落的概率都是$\frac{1}{2}$.分析 (1)记“小球落入A区域”为事件M,“小球落入B区域”为事件N,事件M的对立事件为事件N,小球落入A区域中当且仅当小球一直向左落下或一直向右落下,由此能分别求出小球落入A区域和B区域中的概率.
(2)由题意随机变量X的所有可能的取值为0,1,2,3,且X~B(3,-$\frac{3}{4}$),由此能求出X的分布列和数学期望.
解答 解:(1)记“小球落入A区域”为事件M,“小球落入B区域”为事件N,
则事件M的对立事件为事件N,
而小球落入A区域中当且仅当小球一直向左落下或一直向右落下,
故P(M)=$\frac{1}{8}+\frac{1}{8}$=$\frac{1}{4}$.
∴P(N)=1-P(M)=1-$\frac{1}{4}=\frac{3}{4}$.
(2)由题意随机变量X的所有可能的取值为0,1,2,3,且X~B(3,-$\frac{3}{4}$),
P(X=0)=${C}_{3}^{0}(\frac{1}{4})^{3}=\frac{1}{64}$,
P(X=1)=${C}_{3}^{1}(\frac{1}{4})^{2}(\frac{3}{4})$=$\frac{9}{64}$,
P(X=2)=${C}_{3}^{2}(\frac{1}{4})(\frac{3}{4})^{2}$=$\frac{27}{64}$,
P(X=3)=${C}_{3}^{3}(\frac{3}{4})^{3}$=$\frac{27}{64}$,
∵X的分布列为:
| X | 0 | 1 | 2 | 3$\frac{27}{64}$ |
| P | $\frac{1}{64}$ | $\frac{9}{64}$ | $\frac{27}{64}$ |
点评 本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意二项分布的性质的合理运用.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{{2^{101}}-1}}{{{2^{100}}+1}}$ | B. | $\frac{{{2^{100}}-1}}{{{2^{100}}+1}}$ | C. | $\frac{{{2^{101}}-1}}{{2({{2^{101}}+1})}}$ | D. | $\frac{{{2^{100}}-1}}{{2({{2^{100}}+1})}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{9}{16}$ | B. | $\frac{5}{4}$ | C. | $\frac{21}{16}$ | D. | $\frac{11}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
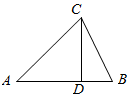 如图,在△ABC中,|$\overrightarrow{CA}$|=$\sqrt{6}$,|$\overrightarrow{CB}$|=2,∠ACB=75°,$\overline{AD}$=λ$\overrightarrow{DB}$
如图,在△ABC中,|$\overrightarrow{CA}$|=$\sqrt{6}$,|$\overrightarrow{CB}$|=2,∠ACB=75°,$\overline{AD}$=λ$\overrightarrow{DB}$查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com