
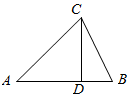
 如图,在△ABC中,|$\overrightarrow{CA}$|=$\sqrt{6}$,|$\overrightarrow{CB}$|=2,∠ACB=75°,$\overline{AD}$=λ$\overrightarrow{DB}$
如图,在△ABC中,|$\overrightarrow{CA}$|=$\sqrt{6}$,|$\overrightarrow{CB}$|=2,∠ACB=75°,$\overline{AD}$=λ$\overrightarrow{DB}$分析 (1)由λ=1,求出$\overrightarrow{C{D}^{2}}=\frac{1}{4}(\overrightarrow{CA}+\overrightarrow{CB})^{2}$=$\frac{1}{4}×(16-2\sqrt{3})$,从而可得到|$\overrightarrow{CD}$|的值;
(2)运用向量的数量积的定义可得$\overrightarrow{CD}•\overrightarrow{AB}$,由向量垂直的条件:数量积为0,即可得λ的值.
解答  解:(1)∵λ=1,∴D为线段AB的中点,
解:(1)∵λ=1,∴D为线段AB的中点,
∴$\overrightarrow{CD}=\frac{1}{2}(\overrightarrow{CA}+\overrightarrow{CB})$,
∴$\overrightarrow{C{D}^{2}}=\frac{1}{4}(\overrightarrow{CA}+\overrightarrow{CB})^{2}$=$\frac{1}{4}(\overrightarrow{C{A}^{2}}+\overrightarrow{C{B}^{2}}+2\overrightarrow{CA}•\overrightarrow{CB})$
=$\frac{1}{4}×(10+2×\sqrt{6}×2cos75°)$=
=$\frac{1}{4}[10+4\sqrt{6}(cos45°cos30°-sin45°sin30°)]$
=$\frac{1}{4}[10+4\sqrt{6}(\frac{\sqrt{2}}{2}×\frac{\sqrt{3}}{2}-\frac{\sqrt{2}}{2}×\frac{1}{2})]$
=$\frac{1}{4}×(16-2\sqrt{3})$.
∴$|\overrightarrow{CD}|=\frac{\sqrt{16-2\sqrt{3}}}{2}$;
(2)∵$\overline{AD}$=λ$\overrightarrow{DB}$,
∴$\overrightarrow{AD}=\frac{λ}{1+λ}\overrightarrow{AB}$,
∴$\overrightarrow{CD}=\overrightarrow{CA}+\overrightarrow{AD}=\overrightarrow{CA}+$$\frac{λ}{1+λ}\overrightarrow{AB}$
=$\overrightarrow{CA}+\frac{λ}{1+λ}(\overrightarrow{CB}-\overrightarrow{CA})$=$\frac{1}{1+λ}\overrightarrow{CA}+\frac{λ}{1+λ}\overrightarrow{CB}$.
∴$\overrightarrow{CD}•\overrightarrow{AB}$=$\frac{1}{1+λ}(\overrightarrow{CA}+λ\overrightarrow{CB})•(\overrightarrow{CB}-\overrightarrow{CA})$=$\frac{1}{1+λ}[λ\overrightarrow{C{B}^{2}}-\overrightarrow{C{A}^{2}}+(1-λ)\overrightarrow{CA}•\overrightarrow{CB}]$
=$\frac{1}{1+λ}[4λ-6+(1-λ)×\sqrt{6}×2cos75°]=0$,
即4λ-6+(1-λ)×$\sqrt{6}×2$cos(45°+30°)=0,
∴4λ-6+(1-λ)×$\sqrt{6}×2$(cos45°cos30°-sin45°sin30°)=0,
∴4λ-6+2$\sqrt{6}$(1-λ)($\frac{\sqrt{2}}{2}×\frac{\sqrt{3}}{2}-\frac{\sqrt{2}}{2}×\frac{1}{2}$)=0.
解得:$λ=\sqrt{3}$.
点评 本题考查向量的模的求法,注意运用向量垂直的条件:数量积为0,注意运用向量共线定理,考查化简整理的运算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
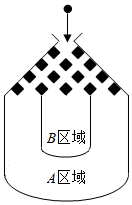 如图,将一个半径适当的小球放入容器上方的入口处,小球自由下落,小球在下落的过程中,将遇到黑色障碍物3次,最后落入A区域或B区域中,已知小球每次遇到障碍物时,向左、右两边下落的概率都是$\frac{1}{2}$.
如图,将一个半径适当的小球放入容器上方的入口处,小球自由下落,小球在下落的过程中,将遇到黑色障碍物3次,最后落入A区域或B区域中,已知小球每次遇到障碍物时,向左、右两边下落的概率都是$\frac{1}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -$\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$或-1 | B. | 2或-1 | C. | 2或1 | D. | 1或-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | A与B是互斥而非对立事件 | B. | A与B是对立事件 | ||
| C. | B与C是互斥而非对立事件 | D. | B与C是对立事件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若m⊥α,m?β,则α⊥β | |
| B. | 若m?α,n?α,m∥β,n∥β,则α∥β | |
| C. | 若m?α,n?α,m,n是异面直线,那么n与α相交 | |
| D. | 若α∩β=m,n∥m,则n∥α且n∥β |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com