
| A. | 若m⊥α,m?β,则α⊥β | |
| B. | 若m?α,n?α,m∥β,n∥β,则α∥β | |
| C. | 若m?α,n?α,m,n是异面直线,那么n与α相交 | |
| D. | 若α∩β=m,n∥m,则n∥α且n∥β |
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:高中数学 来源: 题型:解答题
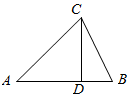 如图,在△ABC中,|$\overrightarrow{CA}$|=$\sqrt{6}$,|$\overrightarrow{CB}$|=2,∠ACB=75°,$\overline{AD}$=λ$\overrightarrow{DB}$
如图,在△ABC中,|$\overrightarrow{CA}$|=$\sqrt{6}$,|$\overrightarrow{CB}$|=2,∠ACB=75°,$\overline{AD}$=λ$\overrightarrow{DB}$查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 180个 | B. | 196个 | C. | 210个 | D. | 224个 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{14}{3}$,$\frac{37}{3}$] | B. | [$\frac{1}{3}$,$\frac{50}{3}$] | C. | [$\frac{11}{3}$,6] | D. | [$\frac{41}{6}$,$\frac{22}{3}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
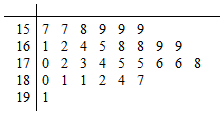 为了解某种树苗培育情况,研究所在苗圃基地花木园中随机抽出30株树苗的主体高,编成如图所示的茎叶图,若苗主体高在169cm以上(包括169cm)定义为“优质苗”,高在169cm以下(不包括169cm)定义为“普苗”
为了解某种树苗培育情况,研究所在苗圃基地花木园中随机抽出30株树苗的主体高,编成如图所示的茎叶图,若苗主体高在169cm以上(包括169cm)定义为“优质苗”,高在169cm以下(不包括169cm)定义为“普苗”查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com