
分析 设椭圆的方程为mx2+ny2=1,(m>0,n>0.m≠n),把已知点的坐标代入方程,求解方程组得到m,n的值,则椭圆方程可求.
解答 解:设椭圆的方程为mx2+ny2=1,(m>0,n>0,m≠n),
∵椭圆经过两点$A(\sqrt{3},-2)$,$B(-2\sqrt{3},1)$,
∴$\left\{\begin{array}{l}{3m+4n=1}\\{12m+n=1}\end{array}\right.$,解得m=$\frac{1}{15}$,n=$\frac{1}{5}$,
∴椭圆的标准方程为$\frac{{x}^{2}}{15}+\frac{{y}^{2}}{5}=1$.
故答案为:$\frac{{x}^{2}}{15}+\frac{{y}^{2}}{5}=1$.
点评 本题考查椭圆方程的求法,注意待定系数法的合理运用,是基础题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ¬P:?x∈(-∞,1)∪(2,+∞),x2-2x-1>0 | B. | ¬P:?x∈[1,2],x2-2x-1>0 | ||
| C. | ¬P:?x∈(-∞,1)∪(2,+∞),x2-2x-1≤0 | D. | ¬P:?x∈[1,2],x2-2x-1≤0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
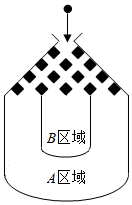 如图,将一个半径适当的小球放入容器上方的入口处,小球自由下落,小球在下落的过程中,将遇到黑色障碍物3次,最后落入A区域或B区域中,已知小球每次遇到障碍物时,向左、右两边下落的概率都是$\frac{1}{2}$.
如图,将一个半径适当的小球放入容器上方的入口处,小球自由下落,小球在下落的过程中,将遇到黑色障碍物3次,最后落入A区域或B区域中,已知小球每次遇到障碍物时,向左、右两边下落的概率都是$\frac{1}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com