
分析 ①,将b的值代入,可得f(x)的解析式,进而根据函数的图象变化的规律,可得其正确;
②,将c的值代入,可得f(x)的解析式,进而由奇函数判断方法,求有f(-x)与-f(x)的关系,分析可得其正确;
③,由②可得函数f(x)=|x|x+bx的奇偶性,进行图象变化可得其正确;
④,举反例|x|x-5x+6=0有三个解-6、2、3,可得其错误.
解答 解:①当b=0,c>0时,f(x)=|x|x+c=$\left\{\begin{array}{l}{x}^{2}+c\\-{x}^{2}+c\end{array}$,结合图形知f(x)=0只有一个实数根,故①正确;
②当c=0时,f(x)=|x|x+bx,有f(-x)=-f(x)=-|x|x-bx,故y=f(x)是奇函数,故②正确;
③y=f(x)的图象可由奇函数f(x)=|x|x+bx,向上或向下平移|c|而得到,y=f(x)的图象与y轴交点为(0,c),故函数y=f(x)的图象关于(0,c)对称,故③正确;
④当b=-5,c=6时,方程|x|x-5x+6=0有三个解-6、2、3,即三个零点,故④错误;
故答案为:①②③.
点评 本题主要考查命题的真假判断,涉及函数的零点、对称性、奇偶性等知识点,注意结合函数的图象与图象的变化进行分析.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 4031 | B. | 4033 | C. | 4034 | D. | 4032 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ③④ | B. | ②③ | C. | ①④ | D. | ①②③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
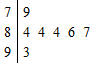 我校为了丰富同学们的课余生活,特举办了一次挑战主持人大赛,如图是七位评委为某选手打出的分数的茎叶图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )
我校为了丰富同学们的课余生活,特举办了一次挑战主持人大赛,如图是七位评委为某选手打出的分数的茎叶图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )| A. | 4;4 | B. | 5;1.6 | C. | 84;4 | D. | 85;1.6 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com