
分析 根据“生长点”的定义建立方程即可求M,结合等差数列的求和公式进行判断即可.
解答 解:若(1,2)为函数f(x)=cos($\frac{π}{2}$x+$\frac{π}{3}$)关于M的一个“生长点”,
则M=f(1)+f(2)+f(3)=cos($\frac{π}{2}$+$\frac{π}{3}$)+cos($\frac{π}{2}$×2+$\frac{π}{3}$)+cos($\frac{π}{2}$×3+$\frac{π}{3}$)
=-sin$\frac{π}{3}$-cos$\frac{π}{3}$+cos(-$\frac{π}{6}$)=-$\frac{\sqrt{3}}{2}$-$\frac{1}{2}$+$\frac{\sqrt{3}}{2}$=-$\frac{1}{2}$,
若f(x)=2x+1,M=105,
则f(m)是公差为2的等差数列,
则由f(m)+f(m+1)+f(m+2)+…+f(m+n)=105
得(n+1)(2m+1)+$\frac{(n+1)•n}{2}×2$=105
即(n+1)(2m+1)+n(n+1)=105,
即(n+1)(2m+n+1)=105,
∵105=1×105=3×35=5×21=7×15,
∴由$\left\{\begin{array}{l}{n+1=3}\\{2m+n+1=35}\end{array}\right.$得$\left\{\begin{array}{l}{n=2}\\{m=16}\end{array}\right.$,此时“生长点”为(2,16),
由$\left\{\begin{array}{l}{n+1=5}\\{2m+n+1=21}\end{array}\right.$得$\left\{\begin{array}{l}{n=4}\\{m=8}\end{array}\right.$,此时“生长点”为(4,8),
由$\left\{\begin{array}{l}{n+1=7}\\{2m+n+1=15}\end{array}\right.$得$\left\{\begin{array}{l}{n=6}\\{m=4}\end{array}\right.$,此时“生长点”为(6,4),
故函数f(x)关于M的“生长点”共有3个,
故答案为:-$\frac{1}{2}$,3
点评 本题主要考查与等差数列有关的新定义问题,读懂题意结合等差数列的求和公式,利用分类讨论的数学思想是解决本题的关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
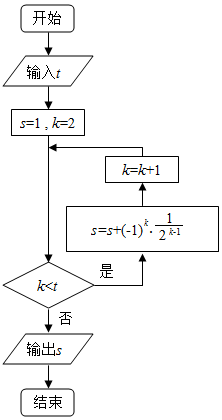
| A. | $\frac{9}{16}$ | B. | $\frac{5}{4}$ | C. | $\frac{21}{16}$ | D. | $\frac{11}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=g(x)是奇函数 | B. | y=g(x)的图象关于点(-$\frac{π}{2}$,0)对称 | ||
| C. | y=g(x)的图象关于直线x=$\frac{π}{2}$对称 | D. | y=g(x)的周期为π |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
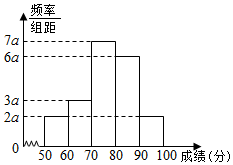 在一次数学竞赛的200名学生考试成绩中利用随机抽样的方法抽取20名学生考试成绩(单位:分)为样本得频率分布直方图如图:
在一次数学竞赛的200名学生考试成绩中利用随机抽样的方法抽取20名学生考试成绩(单位:分)为样本得频率分布直方图如图:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com