
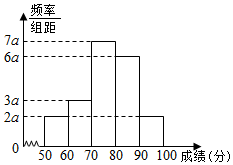
 在一次数学竞赛的200名学生考试成绩中利用随机抽样的方法抽取20名学生考试成绩(单位:分)为样本得频率分布直方图如图:
在一次数学竞赛的200名学生考试成绩中利用随机抽样的方法抽取20名学生考试成绩(单位:分)为样本得频率分布直方图如图:分析 (1)由频率分布直方图的性质得(2a+3a+6a+7a+2a)×10=200a=1,由此能求出a.
(2)先求出分数在60分以下的频率,从而求出这次竞赛不及格的学生人数,求出分数在90分(包括90分)以上的频率,从而能求出这次竞赛优秀的学生人数.
(3)样本中落在[60,70)中的学生人数为3人.设样本中落在[50,60)中的2人成绩为A1,A2,落在[60,70)中的3人为B1,B2,B3.由此能求出此2人的成绩都在[60,70)中的概率.
解答 解:(1)∵组距为10,∴(2a+3a+6a+7a+2a)×10=200a=1,
∴a=$\frac{1}{200}$=0.005.…(2分)
(2)分数在6(0分)以下的频率为2a×10=20a=0.1=10%,
∴这次竞赛不及格的学生人数为0.1×200=20.…(4分)
分数在9(0分)(包括90分)以上的频率为2a×10=20a=0.1=10%,
∴这次竞赛优秀的学生人数为0.1×200=20.…(6分)
(3)∵样本中落在[60,70)中的学生人数为3a×10×20=3×0.005×10×20=3.
∴设样本中落在[50,60)中的2人成绩为A1,A2,落在[60,70)中的3人为B1,B2,B3.
则从[50,70)中选2人共有$C_5^2=\frac{5×4}{2}=10$种选法,
其中2人都在[60,70)中的基本事件有$C_3^2=C_3^1=3$种,
故所求概率p=$\frac{3}{10}$.…(12分)
点评 本题考查频率分布直方图的应用,考查概率的求法,是基础题,解题时要认真审题,注意等可能事件概率计算公式的合理运用.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -$\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$或-1 | B. | 2或-1 | C. | 2或1 | D. | 1或-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | A与B是互斥而非对立事件 | B. | A与B是对立事件 | ||
| C. | B与C是互斥而非对立事件 | D. | B与C是对立事件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-$\frac{1}{8}$,1] | B. | [0,1] | C. | [0,$\frac{1}{4}$] | D. | [-$\frac{1}{9}$,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com