
分析 (1)由两角和的正弦公式及二倍角公式,化简求得f(x)═$\frac{\sqrt{3}}{2}$sin2x-$\frac{1}{2}$,根据正弦函数的图象和性质,求出周期和f(x)的值域;
(2)f(C+$\frac{π}{4}$)=$\frac{\sqrt{3}}{4}$-$\frac{1}{2}$,求得C=$\frac{π}{6}$,由三角形的面积公式求得ab=4$\sqrt{3}$,余弦定理求得a2+b2=16,联立求得a、b的值.
解答 解:(1)f(x)=sin(2x+$\frac{π}{6}$)-cos2x=$\frac{\sqrt{3}}{2}$sin2x+$\frac{1}{2}$cos2x-$\frac{1}{2}$(2cos2x-1)-$\frac{1}{2}$,
=$\frac{\sqrt{3}}{2}$sin2x-$\frac{1}{2}$,
f(x)的最小正周期π,
x∈[$\frac{π}{12}$,$\frac{2π}{3}$],2x∈[$\frac{π}{6}$,$\frac{4π}{3}$],
f(x)的值域[-$\frac{5}{4}$,$\frac{\sqrt{3}}{2}$-$\frac{1}{2}$];
(2)f(x)=$\frac{\sqrt{3}}{2}$sin2x-$\frac{1}{2}$,
f(C+$\frac{π}{4}$)=$\frac{\sqrt{3}}{2}$sin2(C+$\frac{π}{4}$)-$\frac{1}{2}$=$\frac{\sqrt{3}}{4}$-$\frac{1}{2}$,
∴sin(2C+$\frac{π}{2}$)=$\frac{1}{2}$,cos2C=$\frac{1}{2}$,角C为锐角,
C=$\frac{π}{6}$,
S=$\frac{1}{2}absinC$,S△ABC=$\sqrt{3}$,
ab=4$\sqrt{3}$,
由余弦定理可知:c2=a2+b2-2abcosC,
a2+b2=16,
解得b=2,a=2$\sqrt{3}$或b=2$\sqrt{3}$,a=2,
点评 本题考查三角恒等变换,正弦函数图象及性质、余弦定理,过程较繁琐,属于中档题.


科目:高中数学 来源: 题型:解答题
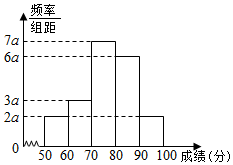 在一次数学竞赛的200名学生考试成绩中利用随机抽样的方法抽取20名学生考试成绩(单位:分)为样本得频率分布直方图如图:
在一次数学竞赛的200名学生考试成绩中利用随机抽样的方法抽取20名学生考试成绩(单位:分)为样本得频率分布直方图如图:查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
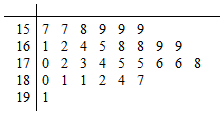 为了解某种树苗培育情况,研究所在苗圃基地花木园中随机抽出30株树苗的主体高,编成如图所示的茎叶图,若苗主体高在169cm以上(包括169cm)定义为“优质苗”,高在169cm以下(不包括169cm)定义为“普苗”
为了解某种树苗培育情况,研究所在苗圃基地花木园中随机抽出30株树苗的主体高,编成如图所示的茎叶图,若苗主体高在169cm以上(包括169cm)定义为“优质苗”,高在169cm以下(不包括169cm)定义为“普苗”查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 等腰三角形 | B. | 等边三角形 | C. | 直角三角形 | D. | 等腰直角三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com