
| A. | [-$\frac{1}{8}$,1] | B. | [0,1] | C. | [0,$\frac{1}{4}$] | D. | [-$\frac{1}{9}$,1] |
分析 由f(c)=(c-a)(c-b)=c2-(a+b)c+ab,缩小后利用配方法求得f(c)的最小值;然后再由基本不等式放大,再由配方法求得f(c)的最大值.
解答 解:f(c)=(c-a)(c-b)=c2-(a+b)c+ab
≥c2-c(a+b)=c2-c(1-c)
=$2(c-\frac{1}{4})^{2}-\frac{1}{8}≥-\frac{1}{8}$,
当c=$\frac{1}{4}$,a=0,b=$\frac{3}{4}$时,f(c)=$-\frac{1}{8}$,
∴f(c)的最小值为-$\frac{1}{8}$;
又f(c)=c2-(1-c)c+ab
$≤{c}^{2}-c+{c}^{2}+(\frac{a+b}{2})^{2}$=$2{c}^{2}-c+(\frac{1-c}{2})^{2}$=$\frac{9}{4}{c}^{2}-\frac{3}{2}c+\frac{1}{4}$
=$\frac{9}{4}(c-\frac{1}{3})^{2}$,
由0≤c=1-a-b≤1,得当c=1时,f(c)有最大值为1.
∴f(c)的取值范围为[$-\frac{1}{8},1$].
故选:A.
点评 本题考查函数值域的求法,训练了利用基本不等式求函数的值域,考查灵活变形能力,属中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
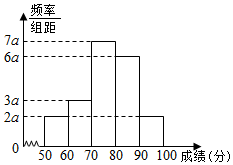 在一次数学竞赛的200名学生考试成绩中利用随机抽样的方法抽取20名学生考试成绩(单位:分)为样本得频率分布直方图如图:
在一次数学竞赛的200名学生考试成绩中利用随机抽样的方法抽取20名学生考试成绩(单位:分)为样本得频率分布直方图如图:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{2}$ | B. | 0 | C. | -$\frac{\sqrt{2}}{2}$ | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 180个 | B. | 196个 | C. | 210个 | D. | 224个 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
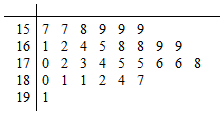 为了解某种树苗培育情况,研究所在苗圃基地花木园中随机抽出30株树苗的主体高,编成如图所示的茎叶图,若苗主体高在169cm以上(包括169cm)定义为“优质苗”,高在169cm以下(不包括169cm)定义为“普苗”
为了解某种树苗培育情况,研究所在苗圃基地花木园中随机抽出30株树苗的主体高,编成如图所示的茎叶图,若苗主体高在169cm以上(包括169cm)定义为“优质苗”,高在169cm以下(不包括169cm)定义为“普苗”查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com