
分析 (Ⅰ) $f'(x)=\frac{2}{x}+2x-a=\frac{{2{x^2}-ax+2}}{x}(x>0)$.令h(x)=2x2-ax+2,△=a2-16.通过①当a≤0时,②当0<a≤4时,③当a>4时,分别判断导函数的符号,判断函数的单调性,求解单调区间.
(Ⅱ)由(Ⅰ)知,a∈[-2,0)时,函数f(x)在区间(0,1]上单调递增,当x∈(0,1]时,求出函数f(x)的最大值是f(1)=3-a,对任意的a∈[-2,0),都存在x0∈(0,1],使得不等式$2m{e^a}(a+1)+f({x_0})>{a^2}+3a+2$成立,转化为:对任意的a∈[-2,0),不等式2mea(a+1)-a2-4a+1>0都成立,记h(a)=2mea(a+1)-a2-4a+1,求出导函数,通过①当m≤1时,判断函数的单调性求出最值,②当m>1时,(ⅰ)当1<m<e2时,(ⅱ)当m≥e2时,通过函数的地址求解m的取值范围.
解答 解:(Ⅰ)$f'(x)=\frac{2}{x}+2x-a=\frac{{2{x^2}-ax+2}}{x}(x>0)$.
令h(x)=2x2-ax+2,△=a2-16.
①当a≤0时,-ax≥0,∴$f'(x)=\frac{h(x)}{x}>0$,函数f(x)在(0,+∞)上单调递增;
②当0<a≤4时,△=a2-16≤0,所以h(x)≥0,函数f(x)在(0,+∞)上单调递增;
③当a>4时,△=a2-16>0,
令h(x)=0,得${x_1}=\frac{{a-\sqrt{{a^2}-16}}}{4}>0,{x_2}=\frac{{a+\sqrt{{a^2}-16}}}{4}>0$,
f′(x)>0⇒x∈(0,x1)∪(x2,+∞);f′(x)<0⇒x∈(x1,x2).
所以,f(x)在(0,x1)和(x2,+∞)上单调递增,在(x1,x2)单调递减.
综上,1°当a≤1时,函数f(x)在(0,+∞)上单调递增;
2°当a>1时,f(x)在(0,x1)和(x2,+∞)上单调递增,在(x1,x2)单调递减.
(注:如果在每种情况中已说明函数在哪个区间上的单调性,不写综上不扣分;如果每种情况只解出不等式,最后没写综上扣1分)
(Ⅱ)由(Ⅰ)知,a∈[-2,0)时,函数f(x)在区间(0,1]上单调递增,
所以当x∈(0,1]时,函数f(x)的最大值是f(1)=3-a,对任意的a∈[-2,0),
都存在x0∈(0,1],使得不等式$2m{e^a}(a+1)+f({x_0})>{a^2}+3a+2$成立,
即对任意的a∈[-2,0),$2m{e^a}(a+1)+f{({x_0})_{max}}>{a^2}+3a+2$都成立,
即对任意的a∈[-2,0),不等式2mea(a+1)-a2-4a+1>0都成立,
记h(a)=2mea(a+1)-a2-4a+1,则h'(a)=2mea(a+2)-2a-4=2(a+2)(mea-1).∵a∈[-2,0),∴${e^a}∈[\frac{1}{e^2},1)$,且a+2≥0.
①当m≤1时,mea-1<0,∴h'(a)≤0,即a∈[-2,0)时,h(a)单调递减.
∴h(a)>0,只需h(0)≥0,解得$m≥-\frac{1}{2}$,∴$m∈[-\frac{1}{2},\;1]$.
②当m>1时,令h'(a)=0得a=-2或a=-lnm,因为a∈[-2,0),所以2(a+2)≥0.
(ⅰ)当1<m<e2时,-lnm∈[-2,0),当a∈(-2,-lnm)时,h'(a)<0;
当a∈(-lnm,0)时,h'(a)>0,∴$h{(a)_{min}}=h(-lnm)=-{ln^2}m+2lnm+3>0$,
解得$m∈(\frac{1}{e},{e^3})$,∴m∈(1,e2).
(ⅱ)当m≥e2时,因为-2≤a<0,所以$\frac{1}{e^2}≤{e^a}<1$,所以mea≥1,所以h'(a)≥0,
则h(a)在[-2,0)上单调递增,得h(-2)=5-2me-2>0,即$m<\frac{{5{e^2}}}{2}$,∴$m∈[{e^2},\frac{{5{e^2}}}{2})$.
综上,m的取值范围是$[-\frac{1}{2},\frac{{5{e^2}}}{2})$.
点评 本题考查函数的导数以及函数的单调性,极值以及最值的关系,构造法的应用,考查转化思想,分类讨论思想的应用,考查分析问题解决问题的能力.


 名师点拨卷系列答案
名师点拨卷系列答案科目:高中数学 来源: 题型:解答题
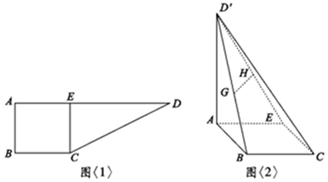 如图<1>:在直角梯形ABCD中,AD∥BC,∠ABC=90°,AB=BC=2,AD=6,CE⊥AD于E点,把△DEC沿CE折到D′EC的位置,使D′A=2$\sqrt{3}$,如图<2>:若G,H分别为D′B,D′E的中点.
如图<1>:在直角梯形ABCD中,AD∥BC,∠ABC=90°,AB=BC=2,AD=6,CE⊥AD于E点,把△DEC沿CE折到D′EC的位置,使D′A=2$\sqrt{3}$,如图<2>:若G,H分别为D′B,D′E的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,-$\frac{1}{2}$) | B. | (-$\frac{1}{2}$,$\frac{1}{3}$) | C. | [0,+∞) | D. | (-$\frac{1}{2}$,-$\frac{1}{4}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
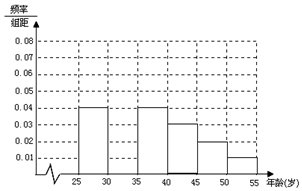 智能手机功能强大,许多人喜欢用手机看电视、看电影.某同学在暑假期间开展社会实践,对[25,55]岁的人群随机抽取1000人调查是否喜欢用手机看电视、看电影,对喜欢用手机看电视、看电影的称为“手机族”,得到如下各年龄段“手机族”人数频率分布直方图:
智能手机功能强大,许多人喜欢用手机看电视、看电影.某同学在暑假期间开展社会实践,对[25,55]岁的人群随机抽取1000人调查是否喜欢用手机看电视、看电影,对喜欢用手机看电视、看电影的称为“手机族”,得到如下各年龄段“手机族”人数频率分布直方图:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{π^2}$ | B. | $1-\frac{4}{π^2}$ | C. | $\frac{4}{π^2}$ | D. | $1-\frac{2}{π^2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com