
分析 对于①②:由n(an+1-an)=2-an+1(n∈N*),变形为(n+1)an+1-nan=2,利用等差数列的通项公式可得:an=2-$\frac{3}{n}$,即可判断出正误.
对于③:(2-a1)+(2-a2)+…+(2-an)=3$(1+\frac{1}{2}+\frac{1}{3}+…+\frac{1}{n})$,由于n→+∞时,1+$\frac{1}{2}+$…+$\frac{1}{n}$→+∞,即可判断出正误;
对于④:(2-an)2=$\frac{9}{{n}^{2}}$<$\frac{9}{n(n-1)}$=9$(\frac{1}{n-1}-\frac{1}{n})$,(n≥2)时,利用“裂项求和”即可判断出正误.
解答 解:对于①②:∵n(an+1-an)=2-an+1(n∈N*),
∴(n+1)an+1-nan=2,
∴数列{nan}是等差数列,首项为-1,公差为2.
∴nan=-1+2(n-1)=2n-3,
解得an=2-$\frac{3}{n}$,
∴数列{an}是单调递增数列,
因此①不正确,②正确.
对于③:(2-a1)+(2-a2)+…+(2-an)=2n-$(2n-\frac{3}{1}-\frac{3}{2}-…-\frac{3}{n})$=3$(1+\frac{1}{2}+\frac{1}{3}+…+\frac{1}{n})$,
由于n→+∞时,1+$\frac{1}{2}+$…+$\frac{1}{n}$→+∞,因此存在n∈N*,使得(2-a1)+(2-a2)+…+(2-an)>2016,正确.
对于④:(2-an)2=$\frac{9}{{n}^{2}}$<$\frac{9}{n(n-1)}$=9$(\frac{1}{n-1}-\frac{1}{n})$,(n≥2)时,
∴n≥2时,(2-a1)2+(2-a2)2+…+(2-an)2<9+9$[(1-\frac{1}{2})+(\frac{1}{2}-\frac{1}{3})$+…+$(\frac{1}{n-1}-\frac{1}{n})]$=9+9$(1-\frac{1}{n})$<18,
因此不存在n∈N*,使得(2-a1)2+(2-a2)2+…+(2-an)2>2016.
综上可得:只有②③正确.
故答案为:②③.
点评 本题考查了等差数列的通项公式、“裂项求和”方法、不等式的性质、“放缩法”、数列的单调性、“调和级数”的性质,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
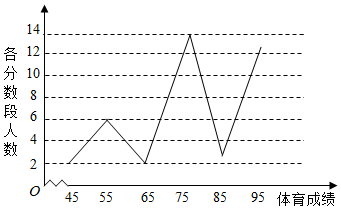 某校高一年级学生全部参加了体育科目的达标测试,现从中随机抽取40名学生的测试成绩,整理数据并按分数段[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]进行分组,假设同一组中的每个数据可用该组区间的中点值代替,则得到体育成绩的折线图(如图).
某校高一年级学生全部参加了体育科目的达标测试,现从中随机抽取40名学生的测试成绩,整理数据并按分数段[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]进行分组,假设同一组中的每个数据可用该组区间的中点值代替,则得到体育成绩的折线图(如图).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com