
分析 (Ⅰ)求导根据导数和函数的单调性的关系即可求出,
(Ⅱ)求导,根据中点坐标公式得到$F'(\frac{{{x_1}+{x_2}}}{2})$=-(x1+x2)+a+$\frac{6}{{x}_{1}+{x}_{2}}$,①,分别把两个零点x1,x2,代入到F(x)中,转化,分离参数得到a-(x1+x2)=$\frac{3ln\frac{{x}_{1}}{{x}_{2}}}{{x}_{2}-{x}_{1}}$,再代入得到$F'(\frac{{{x_1}+{x_2}}}{2})$=$\frac{3}{{x}_{2}-{x}_{1}}$[ln$\frac{{x}_{1}}{{x}_{2}}$+$\frac{2(1-\frac{{x}_{1}}{{x}_{2}})}{1+\frac{{x}_{1}}{{x}_{2}}}$],换元,构造函数得到h(t)=lnt+$\frac{2(1-t)}{1+t}$,根据导数求出h(t)的最大值,即可证明.
解答 解:(Ⅰ)函数的定义域为(0,+∞),
∴f′(x)=2x+a-$\frac{1}{x}$=$\frac{2{x}^{2}+ax-1}{x}$,
令f′(x)>0,得x>$\frac{\sqrt{{a}^{2}+8}+a}{4}$,
f′(x)<0,得0<x<$\frac{\sqrt{{a}^{2}+8}-a}{4}$,
∴函数f(x)在($\frac{\sqrt{{a}^{2}+8}+a}{4}$,+∞)为增函数,在(0,$\frac{\sqrt{{a}^{2}+8}-a}{4}$)为减函数,
(Ⅱ)由已知g(x)=f(x)+2lnx,
∴F(x)=3g(x)-2xg′(x)=-x2+ax+3lnx-2,
∴F′(x)=-2x+a+$\frac{3}{x}$,
即:$F'(\frac{{{x_1}+{x_2}}}{2})$=-(x1+x2)+a+$\frac{6}{{x}_{1}+{x}_{2}}$,①
∵函数F(x)在定义域内有两个零点x1,x2,
∴-x12+ax1+3lnx1-2=0,②
-x22+ax2+3lnx2-2=0,③
②-③得-(x12-x22)+a(x1-x2)+3(lnx1-lnx2)=0
可得(x1-x2)[a-(x1+x2)]+3ln$\frac{{x}_{1}}{{x}_{2}}$=0,
∴a-(x1+x2)=$\frac{3ln\frac{{x}_{1}}{{x}_{2}}}{{x}_{2}-{x}_{1}}$,
代入①得:$F'(\frac{{{x_1}+{x_2}}}{2})$=$\frac{3ln\frac{{x}_{1}}{{x}_{2}}}{{x}_{2}-{x}_{1}}$+$\frac{6}{{x}_{1}+{x}_{2}}$=$\frac{3}{{x}_{2}-{x}_{1}}$[ln$\frac{{x}_{1}}{{x}_{2}}$+$\frac{2({x}_{2}-{x}_{1})}{{x}_{2}+{x}_{1}}$]=$\frac{3}{{x}_{2}-{x}_{1}}$[ln$\frac{{x}_{1}}{{x}_{2}}$+$\frac{2(1-\frac{{x}_{1}}{{x}_{2}})}{1+\frac{{x}_{1}}{{x}_{2}}}$],
令$\frac{{x}_{1}}{{x}_{2}}$=t,则0<t<1,
∴h(t)=lnt+$\frac{2(1-t)}{1+t}$,
∴h′(t)=$\frac{1}{t}$+$\frac{-2(1+t)-2(1-t)}{(1+t)^{2}}$=$\frac{1}{t}$-$\frac{4}{(1+t)^{2}}$=$\frac{(1-t)^{2}}{t(1+t)^{2}}$≥0
∴h(t)在(0,1)上为增函数,
∴h(t)<h(1)=0,
∵x1<x2,
∴$F'(\frac{{{x_1}+{x_2}}}{2})$<0.
点评 本题考查利用导数研究函数的单调性,训练了利用导数求函数的最值,考查数学转化思想方法,考查推理论证能力与运算能力属难题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
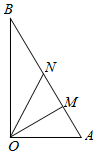 如图所示,某镇有一块空地△OAB,其中OA=3km,OB=3$\sqrt{3}$km,∠AOB=90°.当地镇政府规划将这块空地改造成一个旅游景点,拟在中间挖一个人工湖△OMN,其中M,N都在边AB上,且∠MON=30°,挖出的泥土堆放在△OAM地带上形成假山,剩下的△OBN地带开设儿童游乐场.为安全起见,需在△OAN的一周安装防护网.
如图所示,某镇有一块空地△OAB,其中OA=3km,OB=3$\sqrt{3}$km,∠AOB=90°.当地镇政府规划将这块空地改造成一个旅游景点,拟在中间挖一个人工湖△OMN,其中M,N都在边AB上,且∠MON=30°,挖出的泥土堆放在△OAM地带上形成假山,剩下的△OBN地带开设儿童游乐场.为安全起见,需在△OAN的一周安装防护网.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com