
分析 (1)由三角恒等变换化简f(x),由此得到递增区间.
(2)由等式得到$cosB=\frac{{\sqrt{3}}}{2}$,利用余弦定理及三角形面积公式即可.
解答 解:(Ⅰ)由题意可知,$f(x)=\frac{1}{2}sin2x-\frac{{1+cos({2x+\frac{π}{2}})}}{2}$=$\frac{1}{2}sin2x-\frac{1-sin2x}{2}$=$sin2x-\frac{1}{2}$,
由$2kπ-\frac{π}{2}≤2x≤2kπ+\frac{π}{2},\;\;k∈Z$,
可解得:$kπ-\frac{π}{4}≤x≤kπ+\frac{π}{4},\;\;k∈Z$.
又因为x∈(0,π),
所以f(x)的单调递增区间是$({0,\;\;\frac{π}{4}}]$和$[{\frac{3π}{4},\;\;π})$.
(Ⅱ)由$f({\frac{B}{2}})=sinB-\frac{1}{2}=0$,可得$sinB=\frac{1}{2}$,
由题意知B为锐角,所以$cosB=\frac{{\sqrt{3}}}{2}$,
由余弦定理b2=a2+c2-2accosB,
可得:$1+\sqrt{3}ac={a^2}+{c^2}≥2ac$,即$ac≤2+\sqrt{3}$,且当a=c时等号成立,
因此${S_{△ABC}}=\frac{1}{2}acsinB≤\frac{{2+\sqrt{3}}}{4}$,
所以△ABC面积的最大值为$\frac{{2+\sqrt{3}}}{4}$.
点评 本题考查三角恒等变换,余弦定理及三角形面积公式.


 考前必练系列答案
考前必练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
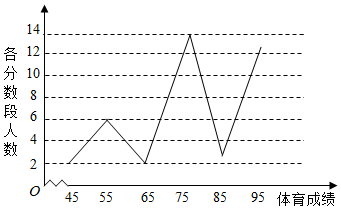 某校高一年级学生全部参加了体育科目的达标测试,现从中随机抽取40名学生的测试成绩,整理数据并按分数段[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]进行分组,假设同一组中的每个数据可用该组区间的中点值代替,则得到体育成绩的折线图(如图).
某校高一年级学生全部参加了体育科目的达标测试,现从中随机抽取40名学生的测试成绩,整理数据并按分数段[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]进行分组,假设同一组中的每个数据可用该组区间的中点值代替,则得到体育成绩的折线图(如图).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某单位利用周末时间组织员工进行一次“健康之路,携手共筑”徒步走健身活动,有n人参加,现将所有参加人员按年龄情况分为[25,30),[30,35],[35,40),[40,45),[45,50),[50,55]六组,其频率分布直方图如图所示.已知[35,40)岁年龄段中的参加者有8人.
某单位利用周末时间组织员工进行一次“健康之路,携手共筑”徒步走健身活动,有n人参加,现将所有参加人员按年龄情况分为[25,30),[30,35],[35,40),[40,45),[45,50),[50,55]六组,其频率分布直方图如图所示.已知[35,40)岁年龄段中的参加者有8人.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5$\sqrt{2}$-7 | B. | 5$\sqrt{2}$-2 | C. | 5$\sqrt{2}$-1 | D. | 5$\sqrt{2}$+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com