
| A. | 5$\sqrt{2}$-7 | B. | 5$\sqrt{2}$-2 | C. | 5$\sqrt{2}$-1 | D. | 5$\sqrt{2}$+1 |
分析 求得圆的圆心M和半径,点P到点Q距离为d≥|PM|-1.运用抛物线的定义可得点P到y轴的距离为|PF|-1,再由当F,P,M三点共线时,取得最小值.计算|FM|,即可得到所求最小值.
解答 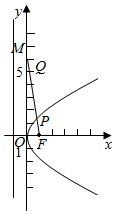 解:设圆心坐标为M(0,7),半径r=1,
解:设圆心坐标为M(0,7),半径r=1,
点P到点Q距离为d,则d≥|PM|-1.
根据抛物线的定义知,点P到y轴的距离为|PF|-1,
两者之和为d+|PF|-1≥|PF|+|PM|-2≥|FM|-2,
当F,P,M三点共线时,取得最小值.
又抛物线焦点F(1,0),|FM|=5$\sqrt{2}$,
则|FM|-2=5$\sqrt{2}$-2,
故所求最小值为5$\sqrt{2}$-2,
故选B.
点评 本题考查抛物线的定义、方程和性质,注意运用转化思想,同时考查三点共线取得最值,考查运算能力,属于中档题.


 科学实验活动册系列答案
科学实验活动册系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
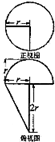 圆锥被一个平面截去一部分,剩余部分再被另一个平面截去一部分后,与半球(半径为r)组成一个几何体,则该几何体三视图中的正视图和俯视图如图所示,若r=1,则该几何体的体积为$\frac{5π}{6}$.
圆锥被一个平面截去一部分,剩余部分再被另一个平面截去一部分后,与半球(半径为r)组成一个几何体,则该几何体三视图中的正视图和俯视图如图所示,若r=1,则该几何体的体积为$\frac{5π}{6}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
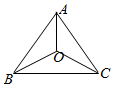 设点O是边长为1的正△ABC的中心(如图所示),则($\overrightarrow{OA}$+$\overrightarrow{OB}$)•($\overrightarrow{OA}$+$\overrightarrow{OC}$)=( )
设点O是边长为1的正△ABC的中心(如图所示),则($\overrightarrow{OA}$+$\overrightarrow{OB}$)•($\overrightarrow{OA}$+$\overrightarrow{OC}$)=( )| A. | $\frac{1}{9}$ | B. | -$\frac{1}{9}$ | C. | -$\frac{1}{6}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com