
分析 (Ⅰ)在方案2中,记“甲河流发生洪水“为事件A,“乙河流发生洪水“为事件B,则P(A)=0.25,P(B)=0.18,由此能求出方案2中损失费ξ(随机变量)的分布列及期望.(Ⅱ)对方案1来说,建围墙需花费1000元,它只能抵御一条河流的洪水,求出该方案中可能的花费,从而得到方案1最好.
解答 解:(Ⅰ)在方案2中,记“甲河流发生洪水“为事件A,“乙河流发生洪水“为事件B,
则P(A)=0.25,P(B)=0.18,
∴有且只有一条河流发生洪水的概率为:
P(A$\overline{B}$+$\overline{A}$B)=P(A)P($\overline{B}$)+P($\overline{A}$)P(B)=0.25×(1-0.18)+(1-0.25)×0.18=0.34,
两河流同时发生洪水的概率为P(AB)=0.25×0.18=0.045,
都不发生洪水的概率为P($\overline{A}\overline{B}$)=(1-0.25)(1-0.18)=0.615,
设损失费为随同变量ξ,则ξ的分布列为:
| ξ | 10000 | 60000 | 0 |
| P | 0.34 | 0.045 | 0.615 |
点评 本题考查离散型随机变量的分布列及数学期望的求法,考查数学期望的应用,是中档题,解题时要认真审题,注意对立事件概率计算公式的合理运用.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
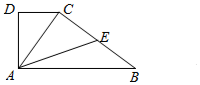 如图,在直角梯形ABCD中,AB∥CD,∠ADC=90°,AB=3,AD=$\sqrt{2}$,E为BC中点,若$\overrightarrow{AB}$•$\overrightarrow{AC}$=3,则$\overrightarrow{AE}$•$\overrightarrow{BC}$=-3.
如图,在直角梯形ABCD中,AB∥CD,∠ADC=90°,AB=3,AD=$\sqrt{2}$,E为BC中点,若$\overrightarrow{AB}$•$\overrightarrow{AC}$=3,则$\overrightarrow{AE}$•$\overrightarrow{BC}$=-3.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5$\sqrt{2}$-7 | B. | 5$\sqrt{2}$-2 | C. | 5$\sqrt{2}$-1 | D. | 5$\sqrt{2}$+1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com