练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    2．已知a∈R，“函数y=3x+a-1有零点”是“函数y=logax在（0，+∞）上为减函数”的（　　）
    A．充分不必要条件B．必要不充分条件
    C．充要条件D．既不充分也不必要条件

    分析 函数y=3x+a-1有零点，可得a=1-3x＜1．由函数y=logax在（0，+∞）上为减函数，可得0＜a＜1．即可判断出结论．

    解答 解：函数y=3x+a-1有零点，则a=1-3x＜1．
    由函数y=logax在（0，+∞）上为减函数，可得0＜a＜1．
    ∴函数y=3x+a-1有零点”是“函数y=logax在（0，+∞）上为减函数”的必要不充分条件．
    故选：B．

    点评 本题考查了函数的单调性、简易逻辑的判定方法，考查了推理能力与计算能力，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

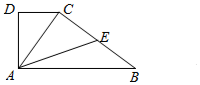    13．如图，在直角梯形ABCD中，AB∥CD，∠ADC=90°，AB=3，AD=$\sqrt{2}$，E为BC中点，若$\overrightarrow{AB}$•$\overrightarrow{AC}$=3，则$\overrightarrow{AE}$•$\overrightarrow{BC}$=-3．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．在△ABC中，角A，B，C的对边分别为a，b，c，且3bsinA=2$\sqrt{3}$asinC．
    （1）若A+3C=π，求sinB的值；
    （2）若c=3，△ABC的面积为3$\sqrt{2}$，求a．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．已知1是lga与lgb的等比中项，若a＞1，b＞1，则ab有（　　）
    A．最小值10B．最小值100C．最大值10D．最大值100

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

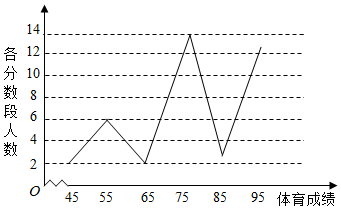    7．某校高一年级学生全部参加了体育科目的达标测试，现从中随机抽取40名学生的测试成绩，整理数据并按分数段[40，50），[50，60），[60，70），[70，80），[80，90），[90，100]进行分组，假设同一组中的每个数据可用该组区间的中点值代替，则得到体育成绩的折线图（如图）．
    （Ⅰ）体育成绩大于或等于70分的学生常被称为“体育良好”．已知该校高一年级有1000名学生，试估计高一年级中“体育良好”的学生人数；
    （Ⅱ）为分析学生平时的体育活动情况，现从体育成绩在[60，70）和[80，90）的样本学生中随机抽取2人，求在抽取的2名学生中，至少有1人体育成绩在[60，70）的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．某单位利用周末时间组织员工进行一次“健康之路，携手共筑”徒步走健身活动，有n人参加，现将所有参加人员按年龄情况分为[25，30），[30，35]，[35，40），[40，45），[45，50），[50，55]六组，其频率分布直方图如图所示．已知[35，40）岁年龄段中的参加者有8人．
    （1）求n的值并补全频率分布直方图；
    （2）从[30，40）岁年龄段中采用分层抽样的方法抽取5人作为活动的组织者，其中选取2人作为领队，在选取的2名领队中至少有1人的年龄在[35，40）内的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．已知点P为抛物线y2=4x上的一个动点，点Q为圆x2+（y-7）2=1上的一个动点，那么点P到点Q的距离与点P到y轴的距离之和的最小值是（　　）
    A．5$\sqrt{2}$-7B．5$\sqrt{2}$-2C．5$\sqrt{2}$-1D．5$\sqrt{2}$+1

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．已知集合M={x|lg（x-2）≤0}，N={x|-1≤x≤3}，则M∪N=（　　）
    A．{x|x≤3}B．{x|2＜x＜3}C．ND．R

    查看答案和解析>>

    同步练习册答案