
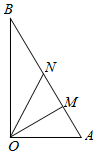 如图所示,某镇有一块空地△OAB,其中OA=3km,OB=3$\sqrt{3}$km,∠AOB=90°.当地镇政府规划将这块空地改造成一个旅游景点,拟在中间挖一个人工湖△OMN,其中M,N都在边AB上,且∠MON=30°,挖出的泥土堆放在△OAM地带上形成假山,剩下的△OBN地带开设儿童游乐场.为安全起见,需在△OAN的一周安装防护网.
如图所示,某镇有一块空地△OAB,其中OA=3km,OB=3$\sqrt{3}$km,∠AOB=90°.当地镇政府规划将这块空地改造成一个旅游景点,拟在中间挖一个人工湖△OMN,其中M,N都在边AB上,且∠MON=30°,挖出的泥土堆放在△OAM地带上形成假山,剩下的△OBN地带开设儿童游乐场.为安全起见,需在△OAN的一周安装防护网.分析 (1)证明△OAN为正三角形,可得△OAN的周长为9,即防护网的总长度为9km;
(2)设∠AOM=θ,在△AOM和△AON中使用正弦定理求出OM,ON,得出△OMN 的面积关于θ的函数,利用三角函数恒等变换化简,得出面积的最小值.
解答 解:(1)∵OA=3km,OB=3$\sqrt{3}$km,∠AOB=90°,∴A=60°,AB=6.
在△OAM中,由余弦定理得:OM2=OA2+AM2-2OA•AM•cosA=$\frac{27}{4}$.
∴OM=$\frac{3\sqrt{3}}{2}$.
由正弦定理得:$\frac{AM}{sin∠AOM}=\frac{OM}{sinA}$,即$\frac{\frac{3}{2}}{sin∠AOM}=\frac{\frac{3\sqrt{3}}{2}}{\frac{\sqrt{3}}{2}}$,
∴sin∠AOM=$\frac{1}{2}$.∴A=30°.
∴∠AON=∠AOM+∠MON=60°.
∴△OAN是等边三角形.
∴△OAN的周长C=3OA=9.
∴防护网的总长度为9km.
(2)设∠AOM=θ(0°<θ<60°),则∠AON=θ+30°,∠OMA=120°-θ,∠ONA=90°-θ.
在△OAM中,由正弦定理得$\frac{OM}{sinA}=\frac{OA}{sin∠OMA}$,即$\frac{OM}{\frac{\sqrt{3}}{2}}$=$\frac{3}{sin(120°-θ)}$=$\frac{3}{sin(60°+θ)}$.
∴OM=$\frac{3\sqrt{3}}{2sin(60°+θ)}$,
在△AON中,由正弦定理得$\frac{ON}{sinA}=\frac{OA}{sin∠ONA}$,即$\frac{ON}{\frac{\sqrt{3}}{2}}=\frac{3}{sin(90°-θ)}$=$\frac{3}{cosθ}$,
∴ON=$\frac{3\sqrt{3}}{2cosθ}$,
∴S△OMN=$\frac{1}{2}OM•ON•sin∠MON$=$\frac{27}{16cosθsin(θ+60°)}$=$\frac{27}{8sin(2θ+60°)+4\sqrt{3}}$.
∴当且仅当2θ+60°=90°,即θ=15°时,△OMN的面积取最小值为$\frac{27}{8+4\sqrt{3}}$=$\frac{27(2-\sqrt{3})}{4}$km2.
点评 本题考查利用数学知识解决三角形问题,考查余弦定理、正弦定理的运用,考查学生分析解决问题的能力,属于中档题.


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com