
分析 (1)设M(x,y),求出MB,MC的斜率,根据条件列方程化简即可开;
(2)设M(x,y),分别求出直线y=x和y=-x的平行线方程,联立方程组解出P,Q的交点坐标,得出|OP|,|OQ|,代入面积公式整理即可得出结论.
解答 解:(1)设M(x,y),则kMB=$\frac{y}{x+2}$,kMC=$\frac{y}{x-2}$.
∵kMB•kMC=1,∴$\frac{{y}^{2}}{{x}^{2}-4}=1$,即$\frac{{x}^{2}}{4}-\frac{{y}^{2}}{4}=1$.
∴动点M的轨迹C的方程为$\frac{{x}^{2}}{4}-\frac{{y}^{2}}{4}=1$.
(2)设M(a,b),则a2-b2=4.
过M与y=x平行的直线方程为y=x-a+b,
联立方程组$\left\{\begin{array}{l}{y=x-a+b}\\{y=-x}\end{array}\right.$,解得P($\frac{a-b}{2}$,$\frac{b-a}{2}$),
同理可得Q($\frac{a+b}{2}$,$\frac{a+b}{2}$).
∴|OP|=$\frac{\sqrt{2}|a-b|}{2}$,|OQ|=$\frac{\sqrt{2}|a+b|}{2}$.
∴SOPMQ=|OP|•|OQ|=$\frac{|{a}^{2}-{b}^{2}|}{2}$=2.
∴平行四边形OPMQ的面积为定值2.
点评 本题考查了轨迹方程的求解,直线的斜率与交点坐标,属于中档题.


科目:高中数学 来源: 题型:解答题
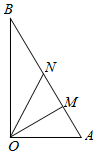 如图所示,某镇有一块空地△OAB,其中OA=3km,OB=3$\sqrt{3}$km,∠AOB=90°.当地镇政府规划将这块空地改造成一个旅游景点,拟在中间挖一个人工湖△OMN,其中M,N都在边AB上,且∠MON=30°,挖出的泥土堆放在△OAM地带上形成假山,剩下的△OBN地带开设儿童游乐场.为安全起见,需在△OAN的一周安装防护网.
如图所示,某镇有一块空地△OAB,其中OA=3km,OB=3$\sqrt{3}$km,∠AOB=90°.当地镇政府规划将这块空地改造成一个旅游景点,拟在中间挖一个人工湖△OMN,其中M,N都在边AB上,且∠MON=30°,挖出的泥土堆放在△OAM地带上形成假山,剩下的△OBN地带开设儿童游乐场.为安全起见,需在△OAN的一周安装防护网.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | -1 | C. | 1 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com