
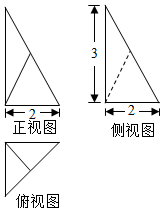
 某多面体是一个四棱锥被一平面截去一部分后得到,它的三视图如图所示,此多面体的体积是( )
某多面体是一个四棱锥被一平面截去一部分后得到,它的三视图如图所示,此多面体的体积是( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 根据三视图画出几何体,由三视图求出几何元素的长度,由分割法和锥体的体积公式求出几何体的体积.
解答 解:根据三视图得,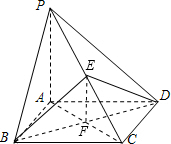
该几何体是过BD且平行于PA的平面截四棱锥P-ABCD所得的几何体,
且PA⊥底面ABCD,底面ABCD为正方形,PA=3、AB=AD=2,
E是PC的中点,则EF=$\frac{1}{2}$PA=$\frac{3}{2}$,
∴截取的部分为三棱锥E-BCD的体积为:
V三棱锥E-BCD=$\frac{1}{3}×\frac{1}{2}×2×2×\frac{3}{2}$=1,
∴多面体的体积V=V四棱锥P-ABCD-V三棱锥E-BCD
=$\frac{1}{3}×2×2×3-1$=3,
故选:B.
点评 本题考查三视图求几何体的体积,由三视图正确复原几何体是解题的关键,考查空间想象能力.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x=0 | B. | x=$\frac{π}{6}$ | C. | x=$\frac{π}{4}$ | D. | x=$\frac{π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 全额分组 | [1,5) | [5,9) | [9,13) | [13,17) | [17,21) | [21,25] |
| 频数 | 3 | 9 | 17 | 11 | 8 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
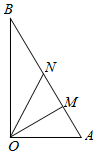 如图所示,某镇有一块空地△OAB,其中OA=3km,OB=3$\sqrt{3}$km,∠AOB=90°.当地镇政府规划将这块空地改造成一个旅游景点,拟在中间挖一个人工湖△OMN,其中M,N都在边AB上,且∠MON=30°,挖出的泥土堆放在△OAM地带上形成假山,剩下的△OBN地带开设儿童游乐场.为安全起见,需在△OAN的一周安装防护网.
如图所示,某镇有一块空地△OAB,其中OA=3km,OB=3$\sqrt{3}$km,∠AOB=90°.当地镇政府规划将这块空地改造成一个旅游景点,拟在中间挖一个人工湖△OMN,其中M,N都在边AB上,且∠MON=30°,挖出的泥土堆放在△OAM地带上形成假山,剩下的△OBN地带开设儿童游乐场.为安全起见,需在△OAN的一周安装防护网.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com