Question

2． 如图所示，一块正方体的木料的上底面有一点E，正方体的棱长为2．
（1）在平面A₁B₁C₁D₁内，请作出过点E与CE垂直的直线l，并证明l⊥CE；
（2）若点E在线段A₁C₁上且C₁E=$\frac{1}{4}$A₁C₁，记（1）中的直线l与CE所确定的平面为α，求点C₁到平面α的距离．

Answer 1

分析 （1）连接C₁E，在平面A₁B₁C₁D₁内，过点E作l⊥C₁E，则l⊥CE．下面给出证明：由正方体可得：CC₁⊥底面A₁B₁C₁D₁，可得CC₁⊥底面A₁B₁C₁D₁，可得CC₁⊥l，又l⊥CE，即可证明l⊥平面CC₁E，l⊥CE．
（2）设直线l分别与C₁D₁、B₁C₁相交于点M，N，连接CM，CN．由（1）可得：l⊥A₁C₁，可得M，N分别为C₁D₁、B₁C₁的中点．平面CC₁E⊥平面CMN．求出点C₁到CE的距离即为点C₁到平面α的距离．

解答 解：（1）连接C₁E，在平面A₁B₁C₁D₁内，过点E作l⊥C₁E，则l⊥CE．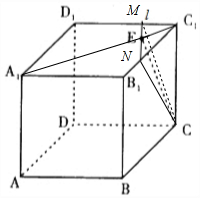
下面给出证明：由正方体可得：CC₁⊥底面A₁B₁C₁D₁，C₁E?底面A₁B₁C₁D₁，
∴CC₁⊥底面A₁B₁C₁D₁，l?底面A₁B₁C₁D₁，
∴CC₁⊥l，又l⊥CE，CC₁∩CE=C，
∴l⊥平面CC₁E，又CE?平面CC₁E．
∴l⊥CE．
（2）设直线l分别与C₁D₁、B₁C₁相交于点M，N，连接CM，CN．
由（1）可得：l⊥A₁C₁，可得M，N分别为C₁D₁、B₁C₁的中点．
平面CC₁E⊥平面CMN．求出点C₁到CE的距离即为点C₁到平面α的距离．
C₁E=$\frac{1}{4}$A₁C₁=$\frac{1}{4}×2\sqrt{2}$=$\frac{\sqrt{2}}{2}$．
在Rt△CC₁E中，CE=$\sqrt{{C}_{1}{C}^{2}+{C}_{1}{E}^{2}}$=$\sqrt{{2}^{2}+（\frac{\sqrt{2}}{2}）^{2}}$=$\frac{3\sqrt{2}}{2}$．
∴点C₁到平面α的距离=$\frac{C{C}_{1}•{C}_{1}E}{CE}$=$\frac{2×\frac{\sqrt{2}}{2}}{\frac{3\sqrt{2}}{2}}$=$\frac{2}{3}$．

点评 本题考查了空间线面位置关系、勾股定理、三角形面积计算公式，考查了推理能力与计算能力，属于中档题．