
| a | n |
| an+3 |
| 4(n+1) |
| b | n |
| a | n |
| a | n |
| an+3 |
| 4(n+1) |
| b | n |
| an+3 |
| 4(n+1) |
| n |
| n+1 |
| 1 |
| 2 |
| 2 |
| 3 |
| 3 |
| 4 |
| 99 |
| 100 |
| 1 |
| 2 |
| 2 |
| 3 |
| 3 |
| 4 |
| 99 |
| 100 |
| 1 |
| 100 |


 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案科目:高中数学 来源: 题型:
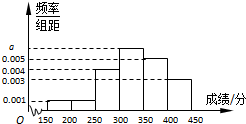 某地区教育主管部门为了对该地区模拟考试成绩进行分析,随机抽取了150分到450分之间的1000名学生的成绩,并根据这1000名学生的成绩画出样本的频率分布直方图(如图),则成绩在[300,350)内的学生人数共有
某地区教育主管部门为了对该地区模拟考试成绩进行分析,随机抽取了150分到450分之间的1000名学生的成绩,并根据这1000名学生的成绩画出样本的频率分布直方图(如图),则成绩在[300,350)内的学生人数共有查看答案和解析>>
科目:高中数学 来源: 题型:
| A、α⊥β,m?α,则m⊥β |
| B、m∥n,n?α,则m∥α |
| C、m⊥α,m?β,则α⊥β |
| D、m∥α,n?a,则m∥n |
查看答案和解析>>
科目:高中数学 来源: 题型:
| lnx+1 |
| ex |
查看答案和解析>>
科目:高中数学 来源: 题型:
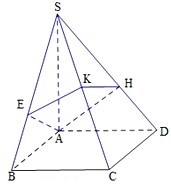 如图,四棱锥S-ABCD的底面是正方形,侧棱SA⊥底面ABCD,过A作AE垂直SB交SB于E点,作AH垂直SD交SD于H点,平面AEH交SC于K点,P是SA上的动点,且AB=1,SA=2.
如图,四棱锥S-ABCD的底面是正方形,侧棱SA⊥底面ABCD,过A作AE垂直SB交SB于E点,作AH垂直SD交SD于H点,平面AEH交SC于K点,P是SA上的动点,且AB=1,SA=2.查看答案和解析>>
科目:高中数学 来源: 题型:
 已知抛物线C:y=x2.过点M(1,2)的直线l交C于A,B两点.抛物线C在点A处的切线与在点B处的切线交于点P.
已知抛物线C:y=x2.过点M(1,2)的直线l交C于A,B两点.抛物线C在点A处的切线与在点B处的切线交于点P.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com