练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知椭圆C的焦点在x轴上，且短轴长为4，离心率e=
    		5
    5
    ，
    （1）求椭圆C的方程；
    （2）若过椭圆C的右焦点F2且斜率为2的直线交椭圆C于A、B两点，求弦AB的长．
    考点：椭圆的简单性质
    专题：圆锥曲线的定义、性质与方程
    分析：（1）设出椭圆C的标准方程，由短轴长与离心率，结合a2=b2-c2，求出b、a，即得标准方程；
    （2）求出直线AB的方程，与椭圆的方程组成方程组，求出点A、B的坐标，计算出弦长|AB|．
    解答： 解：（1）根据题意，设椭圆C的方程为
    x2
    a2
    +
    y2
    b2
    =1（a＞b＞0），
    ∴2b=4，e=
    c
    a
    =
    		5
    5
    ，
    又∵a2=b2-c2，
    ∴b=2，a=
    		5
    ；
    ∴椭圆C的方程为
    x2
    5
    +
    y2
    4
    =1；
    （2）∵椭圆C的右焦点为F2（1，0），
    ∴直线AB的方程为y=2（x-1）；
    ∴
    y=2(x-1)
    x2
    5
    +
    y2
    4
    =1
    ，
    解得
    x=0
    y=-2
    ，或
    x=
    5
    3
    y=
    4
    3
    ；
    ∴点A（0，-2），B（
    5
    3
    ，
    4
    3
    ），
    ∴弦长|AB|=
    		(
    5
    3
    -0)    2    +(
    4
    3
    +2)    2
    =
    5
    		5
    3
    ．
    点评：本题考查了直线与圆锥曲线的应用问题，解题时应熟练地掌握圆锥曲线的几何性质，并能灵活地应用，是基础题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    若平面α的法向量为
    n
    1    =(3，2，1)    ，平面β的法向量为
    n2
    =(-2，0，1)    ，则平面α与β夹角（锐角）的余弦是（　　）
    A、
    		70
    14
    B、
    		70
    10
    C、-
    		70
    14
    D、-
    		70
    10

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在随机抽查某中学高二级140名学生是否晕机的情况中，已知男学生56人，其中晕机有28人；女学生中不会晕机的为56人．不会晕机的男学生中有2人成绩优秀，不会晕机的女生中有4人成绩优秀．
    （1）完成下面2×2列联表的空白处；
    晕机 不会晕机 合计
    男学生 28 56
    女学生 56
    合计 140
    （2）能否在犯错误的概率不超过0.05的前提下认为是否晕机与性别有关系？（k保留三位小数）
    （3）若从不会晕机的6名成绩优秀的学生中随机抽取2人去国外参加数学竞赛，试求所抽取的2人中恰有一人是男学生、一人是女学生的概率．（4分）
    注：①参考公式：K2=
    n(ad-bc)2
    (a+b)(c+d)(a+c)(b+d)
    ，其中n=a+b+c+d．
    ②常用数据表如下：
    P（K2≥k） 0.50 0.40 0.25 0.15 0.10 0.05 0.025 0.010 0.005 0.001
    k 0.455 0.708 1.323 2.072 2.706 3.841 5.024 6.635 7.879 10.828

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知p：直线x-2y+3=0与抛物线y2=ax（a＞0）没有交点；q：方程
    x2
    4-a
    +
    y2
    a-1
    =1    表示椭圆；若p∧q为真命题，试求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知M（x1，y1）是椭圆
    x2
    a2
    +
    y2
    b2
    =1(a＞b＞0)    上任意一点，F为椭圆的右焦点．
    （1）若椭圆的离心率为e，试用e、a、x1表示|MF|，并求|MF|的最值；
    （2）已知直线m与圆x2+y2=b2相切，并与椭圆交于A、B两点，且直线m与圆的切点Q在y轴的右侧，若a=2，b=1，求△ABF的周长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

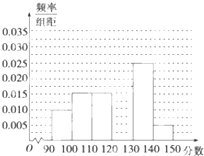    某学校从参加高三模拟考试的学生中随机抽取60名学生，将其数学成绩（均为整数）分成六段[90，100），[100，110），…，[140，150）后得到如下部分频率分布直方图．观察图形的信息，回答下列问题：
    （1）求分数在[120，130）内的频率，并补全这个频率分布直方图（直接画在图形上）；
    （2）统计方法中，同一组数据常用该组区间的中点值作为代表，据此估计本次考试的平均分．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

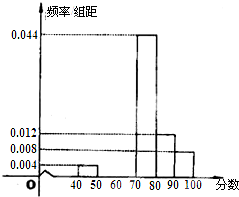    南昌二中某学生社团为了选拔若干名社团义务宣传员，从300名志愿者中随机抽取了50名进行有关知识的测试，成绩（均为整数）按分数段分成六组：第一组[40，50），第二组[50，60），…，第六组[90，100]，第一、二、三组的人数依次构成等差数列，如图是按上述分组方法得到的频率分布直方图的一部分．规定成绩不低于66分的志愿者入选为义务宣传员．
    （1）求第二组、第三组的频率并补充完整频率分布直方图；
    （2）由所抽取志愿者的成绩分布，估计该社团的300名志愿者中有多少人可以入选为义务宣传员？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    某种产品特约经销商根据以往当地的需求情况，得出如图该种产品日需求量的频率分布直方图．
    （Ⅰ）求图中a的值，并估计日需求量的众数；
    （Ⅱ）某日，经销商购进130件该种产品，根据近期市场行情，当天每售出1件能获利30元，未售出的部分，每件亏损20元．设当天的需求量为x件（100≤x≤150），纯利润为S元．
      （ⅰ）将S表示为x的函数；
      （ⅱ）根据直方图估计当天纯利润S不少于3400元的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    一个几何体的三视图如图所示，则这个几何体的表面积为
     
    ．

    查看答案和解析>>

    同步练习册答案