
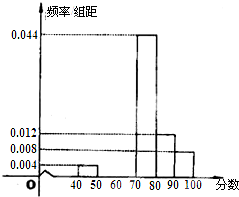
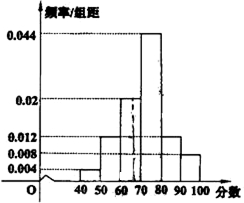
 南昌二中某学生社团为了选拔若干名社团义务宣传员,从300名志愿者中随机抽取了50名进行有关知识的测试,成绩(均为整数)按分数段分成六组:第一组[40,50),第二组[50,60),…,第六组[90,100],第一、二、三组的人数依次构成等差数列,如图是按上述分组方法得到的频率分布直方图的一部分.规定成绩不低于66分的志愿者入选为义务宣传员.
南昌二中某学生社团为了选拔若干名社团义务宣传员,从300名志愿者中随机抽取了50名进行有关知识的测试,成绩(均为整数)按分数段分成六组:第一组[40,50),第二组[50,60),…,第六组[90,100],第一、二、三组的人数依次构成等差数列,如图是按上述分组方法得到的频率分布直方图的一部分.规定成绩不低于66分的志愿者入选为义务宣传员.| 6 |
| 50 |
| 10 |
| 50 |
| 4 |
| 10 |
| 频数 |
| 样本容量 |


 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:高中数学 来源: 题型:
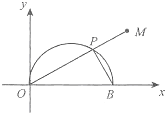 在直角坐标xoy中,以O为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ=2cosθ,如图,曲线C与x轴交于O,B两点,P是曲线C在x轴上方图象上任意一点,连结OP并延长至M,使PM=PB,当P变化时,求动点M的轨迹的长度.
在直角坐标xoy中,以O为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ=2cosθ,如图,曲线C与x轴交于O,B两点,P是曲线C在x轴上方图象上任意一点,连结OP并延长至M,使PM=PB,当P变化时,求动点M的轨迹的长度.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,四棱锥S-ABCD中,ABCD为矩形,SD⊥AD,且SD⊥AB,AD=a(a>0),AB=2AD,SD=
如图,四棱锥S-ABCD中,ABCD为矩形,SD⊥AD,且SD⊥AB,AD=a(a>0),AB=2AD,SD=| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| ||
| 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:

| DP |
| DB |
| π |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
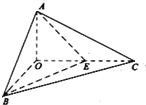 如图,已知三棱锥O-ABC的侧棱OA,OB,OC两两垂直,且OA=1,OB=OC=2,E是OC的中点.
如图,已知三棱锥O-ABC的侧棱OA,OB,OC两两垂直,且OA=1,OB=OC=2,E是OC的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com