
分析 12张牌中抽取2张的方法为C122=66种,其中2张都是2的方法有6种,两张点数之和为6的有22种,分别根据概率公式计算即可.
解答 解:(1)12张牌中抽取2张的方法为C122=66种,其中2张都是2的方法有C42=6种,
故抽出2张都为2的概率为$\frac{6}{66}$=$\frac{1}{11}$;
(2)两张点数之和为6的情况有2种,一种是3+3,另一种是2+4,
抽出2张都为3的有C42=6种,
抽出2张为2和4的方法有4×4=16种,
所以两张点数之和为6的有6+16=22种,
故两张点数之和为6的概率为$\frac{22}{66}$=$\frac{1}{3}$.
点评 本题考查了古典概型的概率问题,关键是求出满足条件的种数,属于基础题.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案科目:高中数学 来源: 题型:选择题
| A. | (1,+∞) | B. | (e,+∞) | C. | (0,1) | D. | (0,e) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
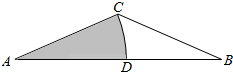 如图,在一个等腰三角形ABC内以A为圆心,腰AC长为半径画弧交底边AB于D,已知AC=1,∠A=30°,现向△ABC内任投一点,该点落在图中阴影部分的概率为$\frac{\sqrt{3}π}{9}$.
如图,在一个等腰三角形ABC内以A为圆心,腰AC长为半径画弧交底边AB于D,已知AC=1,∠A=30°,现向△ABC内任投一点,该点落在图中阴影部分的概率为$\frac{\sqrt{3}π}{9}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ①②③ | C. | ①②④ | D. | ②③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com