
分析 根据已知中对于函数y=f(x),x∈D,若存在常数C,对任意x1∈D,存在唯一的x2∈D,使得$\sqrt{f({x_1})({x_2})}$=M,则称函数f(x)在D上的几何平均数为M.我们易得若函数在区间D上单调递增,则M应该等于函数在区间D上最大值与最小值的几何平均数,由f(x)=x3-x2+1,D=[1,2],代入即可得到答案.
解答 解:根据已知中关于函数f(x)在D上的几何平均数为M的定义,
由于f(x)的导数为f′(x)=3x2-2x,在[1,2]内f′(x)>0,
则f(x)=x3-x2+1在区间[1,2]单调递增,
则x1=1时,存在唯一的x2=2与之对应,
且x=1时,f(x)取得最小值1,x=2时,取得最大值5,
故M=$\sqrt{1×5}$=$\sqrt{5}$.
故答案为:$\sqrt{5}$
点评 此题主要考查了应用新定义分析题意解决问题.对于新定义的问题,需要认真分析定义内容,切记不可偏离题目.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
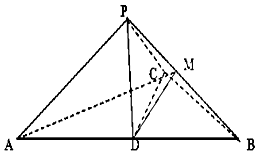 如图,在三棱锥P-ABC中,∠ACB=90°,CB=4,AB=12,D为
如图,在三棱锥P-ABC中,∠ACB=90°,CB=4,AB=12,D为查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$+$\sqrt{2}$i | B. | $\frac{{\sqrt{2}}}{2}$+$\frac{{\sqrt{2}}}{2}$i | C. | 1-i | D. | 1+i |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
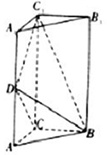 如图,直三棱柱ABC-A1B1C1中,$AC=BC=AD={A_1}D=1,BD=\sqrt{3}$.
如图,直三棱柱ABC-A1B1C1中,$AC=BC=AD={A_1}D=1,BD=\sqrt{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com