
| A. | 若l⊥α,α⊥β,则 l?β | B. | 若l∥α,α∥β,则 l?β | ||
| C. | 若l⊥α,α∥β,则 l⊥β | D. | 若l∥α,α⊥β,则l⊥β |
分析 本题考查的知识点是直线与平面之间的位置关系,逐一分析四个答案中的结论,发现A,B,D中由条件均可能得到l∥β,即A,B,D三个答案均错误,只有C满足平面平行的性质,分析后不难得出答案.
解答 解:若l⊥α,α⊥β,则l?β或l∥β,故A错误;
若l∥α,α∥β,则l?β或l∥β,故B错误;
若l⊥α,α∥β,由平面平行的性质,我们可得l⊥β,故C正确;
若l∥α,α⊥β,则l⊥β或l∥β,故D错误;
故选C.
点评 判断或证明线面平行的常用方法有:①利用线面平行的定义(无公共点);②利用线面平行的判定定理(a?α,b?α,a∥b⇒a∥α);③利用面面平行的性质定理(α∥β,a?α⇒a∥β);④利用面面平行的性质(α∥β,a?α,a?,a∥α⇒?a∥β).线线垂直可由线面垂直的性质推得,直线和平面垂直,这条直线就垂直于平面内所有直线,这是寻找线线垂直的重要依据.垂直问题的证明,其一般规律是“由已知想性质,由求证想判定”,也就是说,根据已知条件去思考有关的性质定理;根据要求证的结论去思考有关的判定定理,往往需要将分析与综合的思路结合起来.


 应用题作业本系列答案
应用题作业本系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
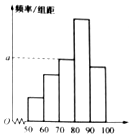 某教师为了分析所任教班级某将考试的成绩,将全班同学的成绩做出了频数与频率的统计表和频率分布直方图.
某教师为了分析所任教班级某将考试的成绩,将全班同学的成绩做出了频数与频率的统计表和频率分布直方图.| 分组 | 频数 | 频率 |
| [50,60) | 3 | 0.06 |
| [60,70) | m | 0.10 |
| [70,80) | 13 | n |
| [80,90) | p | q |
| [90,100] | 9 | 0.18 |
| 总计 | t | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{9π}{8}$,$\frac{5π}{4}$) | B. | [$\frac{5π}{4}$,$\frac{11π}{8}$) | C. | [$\frac{3π}{2}$,$\frac{13π}{8}$) | D. | [$\frac{7π}{4}$,$\frac{15π}{8}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com