
| A�� | 4 | B�� | 3 | C�� | 2 | D�� | 1 |
���� ����֪��f��x��=x3+bx2+cx+d����k��0��k��4ʱ��f��x��-k=0ֻ��һ��ʵ������0��k��4ʱ��f��x��-k=0����������ʵ�����ʺ�����Ϊ����ֵ�����м�Сֵ���Ҽ���ֵΪ4����СֵΪ0��������������ͼ������ʺ���һ�����ĸ����۵������ɵõ��𰸣�
��� �⣺��f��x��=x3+bx2+cx+d��
��k��0��k��4ʱ��f��x��-k=0ֻ��һ��ʵ����
��0��k��4ʱ��f��x��-k=0����������ʵ����
�ʺ�����Ϊ����ֵ�����м�Сֵ���Ҽ���ֵΪ4����СֵΪ0
��f��x��-4=0��f'��x��=0��һ����ͬ��ʵ����������ֵ�㣬�ʣ�1����ȷ��
f��x��=0��f'��x��=0��һ����ͬ��ʵ��������Сֵ�㣬�ʣ�2����ȷ��
f��x��+3=0��һʵ��С�ں�����С����㣬f��x��-1=0������ʵ�������ں�����С����㣬�ʣ�3������
f��x��+3=0��һʵ��С�ں�����С����㣬f��x��-2=0������ʵ�������ں�����С����㣬�ʣ�4������
��ѡ��D��
���� ���⿼���֪ʶ���Ǹ��Ĵ����Լ����ĸ����жϣ����и�����֪�������жϳ�����f��x��=x3+bx2+cx+d��ͼ��������ǽ����Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ABΪֱ���İ�ԲO��ȡһ��C������AC���ӳ����B��������ཻ�ڵ�D����CΪ�е������߽�AB���ӳ�����G����BD��F��
��ͼ����ABΪֱ���İ�ԲO��ȡһ��C������AC���ӳ����B��������ཻ�ڵ�D����CΪ�е������߽�AB���ӳ�����G����BD��F���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
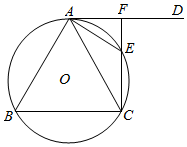 ��ͼ��ʾ����ABC�ڽ��ڡ�O��AD�ǡ�O�����ߣ��е�ΪA����DAC��ƽ���߽���O��E��������AB��AE��
��ͼ��ʾ����ABC�ڽ��ڡ�O��AD�ǡ�O�����ߣ��е�ΪA����DAC��ƽ���߽���O��E��������AB��AE���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ֱ֪��PA���ԲO���ڵ�A��PO����Բ��B��C���㣬AD��PO�ڵ�D��
��ͼ����ֱ֪��PA���ԲO���ڵ�A��PO����Բ��B��C���㣬AD��PO�ڵ�D���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��1��2�� | B�� | ��2��$\root{3}{12}$�� | C�� | ��1��$\root{3}{4}$�� | D�� | ��2��$\root{3}{10}$�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com