
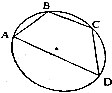
分析 连接AC,在△ABC、△ACD中分别用由余弦定理求AC2,两式右边相等消去AC2,式子两角是互补的,得出角的正弦值,可求出sin∠ADC和AC,利用正弦定理得直径,除以2得半径.
解答  解:连接AC,在△ABC中由余弦定理,得:
解:连接AC,在△ABC中由余弦定理,得:
AC2=AB2+BC2-2AB•BCcos∠ABC=32+32-2×3×3cos∠ABC=18-18cos∠ABC,
在△ACD中由余弦定理,得AC2=AD2+DC2-2AD•DCcos∠ADC
=42+82-2×4×8cos∠ADC=80-64cos∠ADC,
从而得18-18cos∠ABC=80-64cos∠ADC,
又∠ADC=π-∠ABC,故cos∠ADC=$\frac{31}{41}$
sin∠ADC=$\frac{2\sqrt{205}}{41}$,AC=$\frac{\sqrt{180}}{\sqrt{41}}$
所以2R=$\frac{\frac{\sqrt{180}}{\sqrt{41}}}{\frac{2\sqrt{205}}{41}}$=3,
故答案为:3.
点评 本题两次用到余弦定理,衔接点有两处,一是有一条公共边,二是式子中两个角互补,圆内接四边形的对角补,要从图中读出,这点很重要;正弦定理记忆的时候要全面,它的比值是三角形外接圆的直径,知道这一点,问题迎刃而解.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
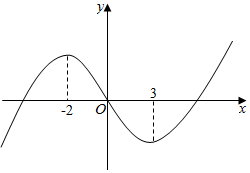
| A. | [0,3) | B. | [-2,3] | C. | (-∞,$\frac{1}{2}$) | D. | (-∞,-2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,0) | B. | (-$\frac{1}{2}$,0) | C. | (-2,0) | D. | (-$\frac{1}{3}$,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | c>b>a | C. | c>a>b | D. | a>c>b |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 20° | B. | 70° | C. | 110° | D. | 160° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com