
| A. | (-1,0) | B. | (-$\frac{1}{2}$,0) | C. | (-2,0) | D. | (-$\frac{1}{3}$,0) |
分析 求出函数f(x)的表达式,作出函数f(x)的图象,用m分别表示出x1,x2,x3,x4,结合分式的性质进行求解即可.
解答 解:f(x)=||x-2|-2|=$\left\{\begin{array}{l}{-x,}&{x<0}\\{x,}&{0≤x≤2}\\{-x+4,}&{2<x<4}\\{x-4,}&{x≥4}\end{array}\right.$,
由图可知,若f(x)=m的四个互不相等的实数根,则m∈(0,2)
且x1,x2,x3,x4分别为: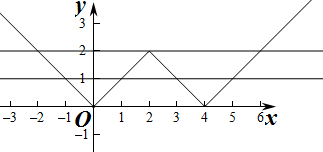
-x1=m,x2=m,-x3+4=m,x4-4=m,
即x1=-m,x2=m,x3=4-m,x4=4+m,
∴$\frac{{{x_1}{x_2}}}{{{x_3}{x_4}}}$=$\frac{-{m}^{2}}{(4-m)(4+m)}$=$\frac{-{m}^{2}}{16-{m}^{2}}$=$\frac{{m}^{2}}{{m}^{2}-16}$
=$\frac{{m}^{2}-16+16}{{m}^{2}-16}$=1+$\frac{16}{{m}^{2}-16}$,
∵m∈(0,2)
∴m2∈(0,4),m2-16∈(-16,-12)
$\frac{16}{{m}^{2}-16}$∈(-$\frac{4}{3}$,-1),
则1+$\frac{16}{{m}^{2}-16}$∈(-$\frac{1}{3}$,0),
即$\frac{{{x_1}{x_2}}}{{{x_3}{x_4}}}$的取值范围是(-$\frac{1}{3}$,0),
故选:D.
点评 本题主要考查函数与方程的应用,作出函数的解析式,利用数形结合分别用m表示出x1,x2,x3,x4的值是解决本题的关键.综合性较强,有一定的难度.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知直线PA与半圆O切于点A,PO交半圆于B,C两点,AD⊥PO于点D.
如图,已知直线PA与半圆O切于点A,PO交半圆于B,C两点,AD⊥PO于点D.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,2) | B. | (-∞,-2) | C. | (-2,+∞) | D. | (-∞,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$f($\frac{π}{4}$)>$\sqrt{3}$f($\frac{π}{3}$) | B. | $\sqrt{2}$f($\frac{π}{4}$)>f($\frac{π}{6}$) | C. | $\sqrt{2}$f($\frac{π}{4}$)<2f($\frac{π}{6}$) | D. | f($\frac{π}{4}$)>$\frac{1}{2}$f($\frac{π}{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com