
分析 在△ABC中,由余弦定理有:BC2=AB2+AC2-2AB•ACcos135°=AB2+AC2+$\sqrt{2}$AB•AC=(AB-AC)2+AB•AC(2+$\sqrt{2}$)
因此:当AB=AC时,BC2有最小值,即BC有最小值,最小值是AB•$\sqrt{2+\sqrt{2}}$,求出AB,即可得出结论.
解答 解:在△ABC中,由余弦定理有:
BC2=AB2+AC2-2AB•ACcos135°=AB2+AC2+$\sqrt{2}$AB•AC=(AB-AC)2+AB•AC(2+$\sqrt{2}$)
因此:当AB=AC时,BC2有最小值,即BC有最小值,最小值是AB•$\sqrt{2+\sqrt{2}}$.
所以:此时根据勾股定理有AB2=1+($\frac{1}{2}$AB•$\sqrt{2+\sqrt{2}}$)2
求得:AB=$\frac{2}{\sqrt{2-\sqrt{2}}}$,
所以:BC=2+2$\sqrt{2}$.
故答案为:2+2$\sqrt{2}$.
点评 本题考查余弦定理的运用,考查学生的计算能力,正确运用余弦定理是关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 一块正方形薄铁片的边长为4cm,以它的一个顶点为圆心,一边长为半径画弧,沿弧剪下一个扇形(如图),用这块扇形铁片围成一个圆锥筒,则这个圆锥筒的容积等于$\frac{\sqrt{15}}{3}$πcm3.
一块正方形薄铁片的边长为4cm,以它的一个顶点为圆心,一边长为半径画弧,沿弧剪下一个扇形(如图),用这块扇形铁片围成一个圆锥筒,则这个圆锥筒的容积等于$\frac{\sqrt{15}}{3}$πcm3.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年龄(岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75) |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 赞成人数 | 4 | 6 | 9 | 6 | 3 | 4 |
| 态度 年龄 | 赞成 | 不赞成 | 总计 |
| 中青年 | |||
| 中老年 | |||
| 总计 |
| X2 | ≤2.706 | >2.706 | >3.841 | >6.635 |
| A、B关联性 | 无关联 | 90% | 95% | 99% |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=g(x)在(0,$\frac{π}{2}$)上递减 | B. | y=g(x)在(0,$\frac{π}{6}$)上递减 | ||
| C. | y=g(x)在(0,$\frac{π}{2}$)上递增 | D. | y=g(x)在(0,$\frac{π}{6}$)上递增 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| A. | 13种 | B. | 21种 | C. | 34种 | D. | 55种 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
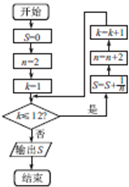
| A. | 求数列{$\frac{1}{n}$}的前11项和(n∈N*) | B. | 求数列{$\frac{1}{2n}$}的前11项和(n∈N*) | ||
| C. | 求数列{$\frac{1}{n}$}的前12项和(n∈N*) | D. | 求数列{$\frac{1}{2n}$的前12项和(n∈N*) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com