
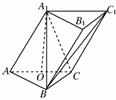
如图,在三棱柱ABC-A1B1C1中,侧面AA1C1C⊥底面ABC,AA1=A1C=AC=2,AB=BC,AB⊥BC,O为AC中点.
(1)证明:A1O⊥平面ABC;
(2)若E是线段A1B上一点,且满足VE-BCC1=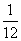 ·VABC-A1B1C1,求A1E的长度.
·VABC-A1B1C1,求A1E的长度.
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:高中数学 来源: 题型:
如图,在边长为4的菱形ABCD中,∠DAB=60°.点E、F分别在边CD、CB上,点E与点C、D不重合,EF⊥AC,EF∩AC=O.沿EF将△CEF翻折到△PEF的位置,使平面PEF⊥平面ABFED.
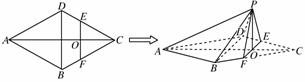
(1)求证:BD⊥平面POA;
(2)记三棱锥P-ABD的体积为V1,四棱锥P-BDEF的体积为V2,求当PB取得最小值时V1∶V2的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
下列说法:
①将一组数据中的每个数据都加上或减去同一个常数后,方差恒不变;
②设有一个回归方程 =3-5x,变量x增加一个单位时,y平均增加5个单位;
=3-5x,变量x增加一个单位时,y平均增加5个单位;
③线性回归方程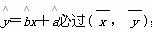 ;
;
④在一个2×2列联表中,由计算得K2=13.079,则有99%的把握确认这两个变量间有关系.
其中错误的个数是( )
A.0 B.1
C.2 D.3
本题可以参考独立性检验临界值表:
| P(K2≥k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com