
如图,在边长为4的菱形ABCD中,∠DAB=60°.点E、F分别在边CD、CB上,点E与点C、D不重合,EF⊥AC,EF∩AC=O.沿EF将△CEF翻折到△PEF的位置,使平面PEF⊥平面ABFED.
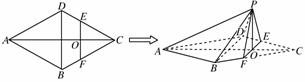
(1)求证:BD⊥平面POA;
(2)记三棱锥P-ABD的体积为V1,四棱锥P-BDEF的体积为V2,求当PB取得最小值时V1∶V2的值.
解析: (1)证明:在菱形ABCD中,∵BD⊥AC,∴BD⊥AO.
∵EF⊥AC,∴PO⊥EF,
∵平面PEF⊥平面ABFED,平面PEF∩平面ABFED=EF,且PO⊂平面PEF,∴PO⊥平面ABFED,
∵BD⊂平面ABFED,∴PO⊥BD.
∵AO∩PO=O,所以BD⊥平面POA.
(2)连接OB,设AO∩BD=H.由(1)知,AC⊥BD.
∵∠DAB=60°,BC=4,∴BH=2,CH=2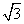 .
.
设OH=x(0<x<2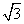 ).
).
由(1)知,PO⊥平面ABFED,∴PO⊥OB,即△POB为直角三角形.
∴PB2=OB2+PO2=(BH2+OH2)+PO2,
∴PB2=4+x2+(2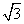 -x)2=2x2-4
-x)2=2x2-4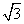 x+16=2(x-
x+16=2(x-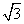 )2+10.
)2+10.
当x=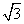 时,PB取得最小值,此时O为CH的中点.
时,PB取得最小值,此时O为CH的中点.
∴S△CEF=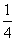 S△BCD,
S△BCD,
∴S梯形BFED=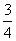 S△BCD=
S△BCD=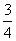 S△ABD,
S△ABD,
∴V1=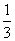 S△ABD·PO,V2=
S△ABD·PO,V2=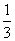 S梯形BFED·PO.
S梯形BFED·PO.
∴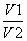 =
=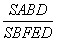 =
=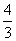 .
.
∴当PB取得最小值时,V1∶V2的值为4∶3.


科目:高中数学 来源: 题型:
如图所示,平行四边形OABC,顶点O、A、C分别表示0、3+2i、-2+4i,试求:
(1) 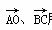 所表示的复数;
所表示的复数;
(2) 对角线 所表示的复数;
所表示的复数;
(3) 求B点对应的复数.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,已知△ABC的面积为14,D、E分别为边AB、BC上的点,且AD∶DB=BE∶EC=2∶1,AE与CD交于P.设存在λ和μ使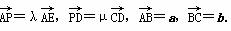
(1) 求λ及μ;
(2) 用a、b表示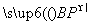 ;
;
(3) 求△PAC的面积.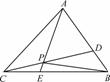
查看答案和解析>>
科目:高中数学 来源: 题型:
如图所示,在四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°,将△ABD沿BD折起,使平面ABD⊥平面BCD,构成三棱锥A-BCD,则在三棱锥A-BCD中,下列命题正确的是( )
A.平面ABD⊥平面ABC B.平面ADC⊥平面BDC
C.平面ABC⊥平面BDC D.平面ADC⊥平面ABC
查看答案和解析>>
科目:高中数学 来源: 题型:
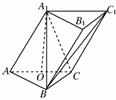
如图,在三棱柱ABC-A1B1C1中,侧面AA1C1C⊥底面ABC,AA1=A1C=AC=2,AB=BC,AB⊥BC,O为AC中点.
(1)证明:A1O⊥平面ABC;
(2)若E是线段A1B上一点,且满足VE-BCC1=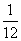 ·VABC-A1B1C1,求A1E的长度.
·VABC-A1B1C1,求A1E的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
某苗圃基地为了解基地内甲、乙两块地种植的同一种树苗的长势情况,从两块地各随机抽取了10株树苗,用茎叶图表示上述两组数据,对两块地抽取树苗的高度的平均数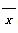 甲、
甲、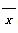 乙和中位数y甲、y乙进行比较,下面结论正确的是( )
乙和中位数y甲、y乙进行比较,下面结论正确的是( )

查看答案和解析>>
科目:高中数学 来源: 题型:
右图是根据部分城市某年6月份的平均气温(单位:℃)数据得到的样本频率分布直方图,其中平均气温的范围是[20.5,26.5],样本数据的分组为[20.5,21.5),[21.5,22.5),[22.5,23.5),[23.5,24.5),[24.5,25.5),[25.5,26.5].已知样本中平均气温低于22.5 ℃的城市个数为11,则样本中平均气温不低于25.5 ℃的城市个数为________.
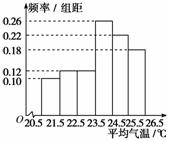
查看答案和解析>>
科目:高中数学 来源: 题型:
将函数f(x)=sin(2x+θ) 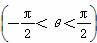 的图象向右平移φ(φ>0)个单位长度后得到函数g(x)的图象,若f(x),g(x)的图象都经过点P
的图象向右平移φ(φ>0)个单位长度后得到函数g(x)的图象,若f(x),g(x)的图象都经过点P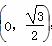 ,则φ的值可以是( )
,则φ的值可以是( )
A. 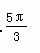 B.
B. 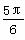
C.  D.
D. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com