
将函数f(x)=sin(2x+θ) 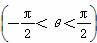 的图象向右平移φ(φ>0)个单位长度后得到函数g(x)的图象,若f(x),g(x)的图象都经过点P
的图象向右平移φ(φ>0)个单位长度后得到函数g(x)的图象,若f(x),g(x)的图象都经过点P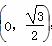 ,则φ的值可以是( )
,则φ的值可以是( )
A. 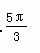 B.
B. 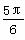
C.  D.
D. 
科目:高中数学 来源: 题型:
已知平面上三个向量a、b、c的模均为1,它们相互之间的夹角均为120°.
(1) 求证:(a-b)⊥c;
(2) 若|ka+b+c|>1(k∈R),求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,在边长为4的菱形ABCD中,∠DAB=60°.点E、F分别在边CD、CB上,点E与点C、D不重合,EF⊥AC,EF∩AC=O.沿EF将△CEF翻折到△PEF的位置,使平面PEF⊥平面ABFED.
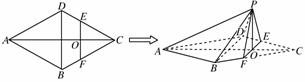
(1)求证:BD⊥平面POA;
(2)记三棱锥P-ABD的体积为V1,四棱锥P-BDEF的体积为V2,求当PB取得最小值时V1∶V2的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
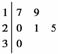
某车间共有12名工人,随机抽取6名,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数.
(1)根据茎叶图计算样本均值.
(2)日加工零件个数大于样本均值的工人为优秀工人.根据茎叶图推断该车间12名工人中有几名优秀工人?
(3)从该车间12名工人中,任取2人,求恰有1名优秀工人的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)=2sin2 -
-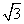 cos 2x-1(x∈R).
cos 2x-1(x∈R).
(1)若函数h(x)=f(x+t)的图象关于点 对称,且t∈(0,π),求t的值;
对称,且t∈(0,π),求t的值;
(2)设p:x∈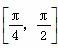 ,q:|f(x)-m|<3,若p是q的充分不必要条件,求实数m的取值范围.
,q:|f(x)-m|<3,若p是q的充分不必要条件,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知圆C经过点A(-2,0),B(0,2),且圆心C在直线y=x上,又直线l:y=kx+1与圆C相交于P、Q两点.
(1)求圆C的方程;
(2)若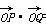 =-2,求实数k的值.
=-2,求实数k的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com