
已知平面上三个向量a、b、c的模均为1,它们相互之间的夹角均为120°.
(1) 求证:(a-b)⊥c;
(2) 若|ka+b+c|>1(k∈R),求k的取值范围.
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:高中数学 来源: 题型:
已知等比数列{an}满足an+1+an=9·2n-1,n∈N*.
(1)求数列{an}的通项公式;
(2)设数列{an}的前n项和为Sn,若不等式Sn>kan-2对一切n∈N*恒成立,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图所示,平行四边形OABC,顶点O、A、C分别表示0、3+2i、-2+4i,试求:
(1) 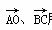 所表示的复数;
所表示的复数;
(2) 对角线 所表示的复数;
所表示的复数;
(3) 求B点对应的复数.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知|a|=4,|b|=3,(2a-3b)·(2a+b)=61.
(1) 求a与b的夹角θ;
(2) 求|a+b|;
(3) 若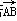 =a,
=a,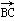 =b,求△ABC的面积.
=b,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,已知△ABC的面积为14,D、E分别为边AB、BC上的点,且AD∶DB=BE∶EC=2∶1,AE与CD交于P.设存在λ和μ使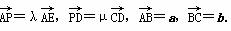
(1) 求λ及μ;
(2) 用a、b表示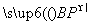 ;
;
(3) 求△PAC的面积.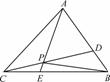
查看答案和解析>>
科目:高中数学 来源: 题型:
如图所示,在四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°,将△ABD沿BD折起,使平面ABD⊥平面BCD,构成三棱锥A-BCD,则在三棱锥A-BCD中,下列命题正确的是( )
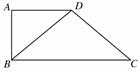
A.平面ABD⊥平面ABC B.平面ADC⊥平面BDC
C.平面ABC⊥平面BDC D.平面ADC⊥平面ABC
查看答案和解析>>
科目:高中数学 来源: 题型:
将函数f(x)=sin(2x+θ) 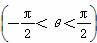 的图象向右平移φ(φ>0)个单位长度后得到函数g(x)的图象,若f(x),g(x)的图象都经过点P
的图象向右平移φ(φ>0)个单位长度后得到函数g(x)的图象,若f(x),g(x)的图象都经过点P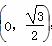 ,则φ的值可以是( )
,则φ的值可以是( )
A. 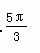 B.
B. 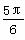
C.  D.
D. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com