练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知|a|＝4，|b|＝3，(2a－3b)·(2a＋b)＝61.

    (1) 求a与b的夹角θ；

    (2) 求|a＋b|；

    (3) 若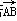＝a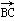，＝b，求△ABC的面积．


    解：(1) ∵  (2a－3b)·(2a＋b)＝61，

    ∴  4|a|2－4a·b－3|b|2＝61.

    又|a|＝4，|b|＝3，∴  64－4a·b－27＝61，

    ∴  a·b＝－6.

    ∴  cosθ＝＝＝－.

    又0≤θ≤π，∴  θ＝.

    (2) 可先平方转化为向量的数量积．

    |a＋b|2＝(a＋b)2＝|a|2＋2a·b＋|b|2

    ＝42＋2×(－6)＋32＝13，

    ∴  |a＋b|＝.

    (3) ∵  与的夹角θ＝，

    ∴  ∠ABC＝π－＝.

    又||＝|a|＝4，||＝|b|＝3，

    ∴  S△ABC＝||||sin∠ABC＝×4×3×＝3.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    已知数列{an}的前n项和Sn＝an－1(a≠0)，则{an}(　　)

    A．一定是等差数列

    B．一定是等比数列

    C．或者是等差数列，或者是等比数列

    D．既不可能是等差数列，也不可能是等比数列

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    复数z＝＋i的共轭复数为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知复数z＝(i是虚数单位)，则|z|＝________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知向量a，b满足|a|＝1，|b|＝2，a与b的夹角为60°，则|a－b|＝________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


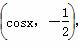    已知向量a＝，b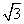＝(sinx，cos2x)，x∈R, 设函数f(x)＝a·b.

    (1) 求f (x)的最小正周期.

    (2) 求f (x) 在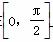上的最大值和最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知平面上三个向量a、b、c的模均为1，它们相互之间的夹角均为120°.

    (1) 求证：(a－b)⊥c；

    (2) 若|ka＋b＋c|＞1(k∈R)，求k的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在△ABC中，过中线AD中点E任作一条直线分别交边AB、AC于M、N两点，设， (xy≠0)，则4x＋y的最小值是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


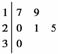
    某车间共有12名工人，随机抽取6名，他们某日加工零件个数的茎叶图如图所示，其中茎为十位数，叶为个位数．

    (1)根据茎叶图计算样本均值．

    (2)日加工零件个数大于样本均值的工人为优秀工人．根据茎叶图推断该车间12名工人中有几名优秀工人？

    (3)从该车间12名工人中，任取2人，求恰有1名优秀工人的概率．

    查看答案和解析>>

    同步练习册答案