练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    复数z＝＋i的共轭复数为________．


    －i

    解析：∵  z＝＋i，∴  z －＝－i.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    给出下列四个结论：

    ①命题“∃x∈R，x2－x＞0”的否定是“∀x∈R，x2－x≤0”；

    ②函数f(x)＝x－sin x(x∈R)有3个零点；

    ③对于任意实数x，有f(－x)＝－f(x)，g(－x)＝g(x)，且x＞0时，f′(x)＞0，g′(x)＞0，则x＜0时，f′(x)＞g′(x)．

    其中正确结论的序号是________．(请写出所有正确结论的序号)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知等比数列{an}满足an＋1＋an＝9·2n－1，n∈N*.

    (1)求数列{an}的通项公式；

    (2)设数列{an}的前n项和为Sn，若不等式Sn＞kan－2对一切n∈N*恒成立，求实数k的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设函数f(x)＝ .

    (1)当a＝－5时，求函数f(x)的定义域；

    (2)若函数f(x)的定义域为R，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图，已知⊙O和⊙M相交于A，B两点，AD为⊙M的直径，直线BD交⊙O于点C，点G为弧BD的中点，连接AG分别交⊙O，BD于点E，F，连接CE.求证：

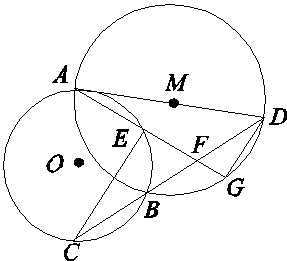
    (1)AG·EF＝CE·GD；

    (2)

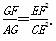
    查看答案和解析>>

    科目：高中数学 来源： 题型：


    　已知复数z＝＋(m2－5m－6)i(m∈R)，试求实数m分别取什么值时，z分别为：

    (1) 实数；

    (2) 虚数；

    (3) 纯虚数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图所示，平行四边形OABC，顶点O、A、C分别表示0、3＋2i、－2＋4i，试求：

    (1) 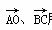所表示的复数；

    (2) 对角线所表示的复数；

    (3) 求B点对应的复数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知|a|＝4，|b|＝3，(2a－3b)·(2a＋b)＝61.

    (1) 求a与b的夹角θ；

    (2) 求|a＋b|；

    (3) 若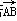＝a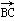，＝b，求△ABC的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图所示，在四边形ABCD中，AD∥BC，AD＝AB，∠BCD＝45°，∠BAD＝90°，将△ABD沿BD折起，使平面ABD⊥平面BCD，构成三棱锥A－BCD，则在三棱锥A－BCD中，下列命题正确的是(　　)

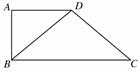
    A．平面ABD⊥平面ABC              B．平面ADC⊥平面BDC

    C．平面ABC⊥平面BDC              D．平面ADC⊥平面ABC

    查看答案和解析>>

    同步练习册答案