练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知数列{an}的前n项和Sn＝an－1(a≠0)，则{an}(　　)

    A．一定是等差数列

    B．一定是等比数列

    C．或者是等差数列，或者是等比数列

    D．既不可能是等差数列，也不可能是等比数列


    C　命题立意：等差数列和等比数列的基本运算是高考经常考查的重点，本题根据数列的前n项和求解通项公式，渗透等差数列和等比数列的定义，体现了基本知识的应用，同时也体现了分类讨论的思想，对能力要求较高，应予以重视．

    解题思路：∵ Sn＝an－1(a≠0)，∴ an＝当a＝1时，an＝0，数列{an}是一个常数列，也是等差数列；当a≠1时，数列{an}是一个等比数列，故选C.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    根据如图所示的伪代码，最后输出的S的值为________．

    S→0

    For I From 1 to 28 Step 3

      S←S＋I

    End For

    Print S

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    给出下列四个结论：

    ①命题“∃x∈R，x2－x＞0”的否定是“∀x∈R，x2－x≤0”；

    ②函数f(x)＝x－sin x(x∈R)有3个零点；

    ③对于任意实数x，有f(－x)＝－f(x)，g(－x)＝g(x)，且x＞0时，f′(x)＞0，g′(x)＞0，则x＜0时，f′(x)＞g′(x)．

    其中正确结论的序号是________．(请写出所有正确结论的序号)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知一个三棱柱，其底面是正三角形，且侧棱与底面垂直，一个体积为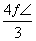的球体与棱柱的所有面均相切，那么这个三棱柱的表面积是(　　)

    A．6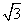                                 B．12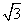 

    C．18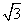                                D．24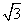

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如果一个棱锥的底面是正多边形，并且顶点在底面的射影是底面的中心，这样的棱锥叫做正棱锥．已知一个正六棱锥的各个顶点都在半径为3的球面上，则该正六棱锥的体积的最大值为______．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知数列{an}中，a1＝1，an＋1＝(－1)n(an＋1)，记Sn为{an}前n项的和，则S2 013＝________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知等比数列{an}满足an＋1＋an＝9·2n－1，n∈N*.

    (1)求数列{an}的通项公式；

    (2)设数列{an}的前n项和为Sn，若不等式Sn＞kan－2对一切n∈N*恒成立，求实数k的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设函数f(x)＝ .

    (1)当a＝－5时，求函数f(x)的定义域；

    (2)若函数f(x)的定义域为R，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知|a|＝4，|b|＝3，(2a－3b)·(2a＋b)＝61.

    (1) 求a与b的夹角θ；

    (2) 求|a＋b|；

    (3) 若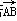＝a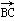，＝b，求△ABC的面积．

    查看答案和解析>>

    同步练习册答案