
已知圆C经过点A(-2,0),B(0,2),且圆心C在直线y=x上,又直线l:y=kx+1与圆C相交于P、Q两点.
(1)求圆C的方程;
(2)若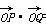 =-2,求实数k的值.
=-2,求实数k的值.
科目:高中数学 来源: 题型:
如图所示,在四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°,将△ABD沿BD折起,使平面ABD⊥平面BCD,构成三棱锥A-BCD,则在三棱锥A-BCD中,下列命题正确的是( )
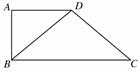
A.平面ABD⊥平面ABC B.平面ADC⊥平面BDC
C.平面ABC⊥平面BDC D.平面ADC⊥平面ABC
查看答案和解析>>
科目:高中数学 来源: 题型:
将函数f(x)=sin(2x+θ) 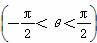 的图象向右平移φ(φ>0)个单位长度后得到函数g(x)的图象,若f(x),g(x)的图象都经过点P
的图象向右平移φ(φ>0)个单位长度后得到函数g(x)的图象,若f(x),g(x)的图象都经过点P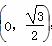 ,则φ的值可以是( )
,则φ的值可以是( )
A. 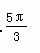 B.
B. 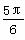
C.  D.
D. 
查看答案和解析>>
科目:高中数学 来源: 题型:
已知双曲线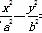 =1和椭圆
=1和椭圆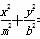 =1(a>0,m>b>0)的离心率互为倒数,那么以a,b,m为边长的三角形是( )
=1(a>0,m>b>0)的离心率互为倒数,那么以a,b,m为边长的三角形是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.锐角或钝角三角形
查看答案和解析>>
科目:高中数学 来源: 题型:
已知椭圆C: =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,其左、右焦点分别是F1、F2,过点F1的直线l交椭圆C于E、G两点,且△EGF2的周长为4
,其左、右焦点分别是F1、F2,过点F1的直线l交椭圆C于E、G两点,且△EGF2的周长为4 .
.
(1)求椭圆C的方程;
(2)若过点M(2,0)的直线与椭圆C相交于两点A、B,设P为椭圆上一点,且满足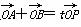 (O为坐标原点),当
(O为坐标原点),当 <
<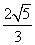 时,求实数t的取值范围.
时,求实数t的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com