
分析 (Ⅰ)讨论2x-3≥0或2x-3<0,求出不等式|2x-3|<x的解集,得出不等式x2-mx+n<0的解集,利用根与系数的关系求出m、n的值;
(Ⅱ)根据a、b、c∈(0,1),且ab+bc+ac=1,求出(a+b+c)2的最小值,即可得出a+b+c的最小值.
解答 解:(Ⅰ)当2x-3≥0,即x≥$\frac{3}{2}$时,不等式|2x-3|<x可化为2x-3<x,
解得x<3,∴$\frac{3}{2}$≤x<3;
当2x-3<0,即x<$\frac{3}{2}$时,不等式|2x-3|<x可化为3-2x<x,
解得x>1,∴1<x<$\frac{3}{2}$;
综上,不等式的解集为{x|1<x<3};
∴不等式x2-mx+n<0的解集为{x|1<x<3},
∴方程x2-mx+n=0的两实数根为1和3,
∴$\left\{\begin{array}{l}{m=1+3=4}\\{n=1×3=3}\end{array}\right.$,
∴m-n=4-3=1;
(Ⅱ)a、b、c∈(0,1),且ab+bc+ac=m-n=1,
∴(a+b+c)2=a2+b2+c2+2(ab+bc+ca)
≥$\frac{1}{2}$(2ab+2bc+2ac)+2(ab+bc+ac)
=3(ab+bc+ca)=3;
∴a+b+c的最小值是$\sqrt{3}$.
点评 本题考查了解不等式以及根与系数的关系应用问题,也考查了基本不等式的应用问题,是综合题.


 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
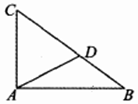 如图,在△ABC中,∠BAC=90°,点D为斜边BC上一点,且AC=CD=2.
如图,在△ABC中,∠BAC=90°,点D为斜边BC上一点,且AC=CD=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x=$\frac{π}{3}$ | B. | x=$\frac{π}{6}$ | C. | x=-$\frac{π}{6}$ | D. | x=-$\frac{π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{8}{25}$ | D. | 与点P的位置有关 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
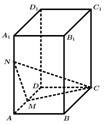 如图,在长方体ABCD-A1B1C1D1中,AA1=6,AB=3,AD=8,点M是棱AD的中点,点N在棱AA1上,且满足AN=2NA1,P是侧面四边形ADD1A1内一动点(含边界),若C1P∥平面CMN,则线段C1P长度的取值范围是( )
如图,在长方体ABCD-A1B1C1D1中,AA1=6,AB=3,AD=8,点M是棱AD的中点,点N在棱AA1上,且满足AN=2NA1,P是侧面四边形ADD1A1内一动点(含边界),若C1P∥平面CMN,则线段C1P长度的取值范围是( )| A. | $[{\sqrt{17},5}]$ | B. | [4,5] | C. | [3,5] | D. | $[{3,\sqrt{17}}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
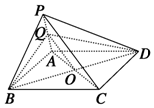
| A. | OQ∥平面PCD | B. | PC∥平面BDQ | C. | AQ∥平面PCD | D. | CD∥平面PAB |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com